Antípoda

Sobre a superfície de uma esfera, dois pontos antipodais são dois diametralmente opostos. Um ponto antipodal é frequentemente designado de antípoda.

Etimologia

O termo antípoda designa tradicionalmente na Europa as regiões situadas do outro lado da Terra, como a Oceania e vem do plural Antípodas. Este termo veio de uma expressão grega significando literalmente "pés opostos" (as pessoas que habitariam nos antípodas caminhariam "ao contrário"). Antípoda é um abuso de linguagem, já que o singular de antipodes é, em grego, antipous.

Na Terra

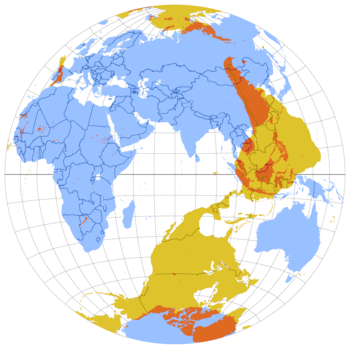
Mapa-múndi (vermelho) ao qual se sobrepôs um mapa antipodal (amarelo) a fim de fazer sobressair o antípoda de cada ponto do globo

Sobre a Terra, apenas 4% da superfície possui pontos antipodais situados ambos em terras emersas. Em 46% dos casos, ambos os pontos antipodais são situados nos oceanos, e os restantes 50% são mistos.

Existe o arquipélago das Ilhas Antípodas, situado a Sul da Nova Zelândia, assim chamadas porque se situam na região antipodal da Grã-Bretanha (embora na realidade o ponto antípoda seja Cherbourg, na França).

Antípodas terrestres

Dos 4% dos antípodas que são ambos terrestres, os pontos mais significativos são os seguintes:

"bordas" da Antártica com partes do extremo norte do Alasca, extremo noroeste e norte insular do Canadá, quase toda Groenlândia, extremo norte da Noruega e da Rússia (parte da ilha do Óblast de Arkhangelsk, norte de Iamália e do Krai de Krasnoiarsk)
Ilha Norte da Nova Zelândia com Espanha
Ilha Sul da Nova Zelândia com Portugal e com a Galiza
Uruguai com Coreia do Sul,
Sudeste do Sudeste Asiático (antiga Indochina), Filipinas, sul do Vietnã, Camboja, Malásia, Singapura, extremo sul da Tailândia, quase toda Indonésia com trecho do oeste da Amazônia (com Bornéu), partes do Brasil, Peru, Colômbia, Venezuela e Guiana
Chile, Argentina e Paraguai com Taiwan, trecho significativo da China, leste da Mongólia, parte da Rússia (com Terra do Fogo)
Sudoeste da Austrália com Bermudas

Conforme acima, são insignificantes (pequenas ilhas) os antípodas terrestres da Europa, Austrália e África.

As maiores extensões contínuas de antípodas somente terrestres são aquela entre Chile e Argentina com a China com cerca de 3,5 milhões km² e aquela entre Groenlândia e leste da Antártica (Terra de Wilkes) com cerca de 2 milhões km².

Localidades antípodas

Mapa mundial das antípodas de terras emergidas. Em cor alaranjado estão marcadas as terras emergidas, com seus nomes respetivos. Na cor branco aparecem as terras emergidas sem seus correspondentes antípodas e na cor azul as superfícies submersas.

Eis uma pequena lista de locais e respetivos antípodas:

Mogadouro (Portugal) e Nelson (Nova Zelândia)
Hamilton (Nova Zelândia) e Córdoba (Espanha)
Guarda (Portugal) e Puponga (Nova Zelândia)
Madrid (Espanha) e Weber (Tararua, Manawatu-Wanganui, (Nova Zelândia)
Wellington (Nova Zelândia) e Alaejos (Espanha)
Baños de la Encina (Espanha) e Rotorua (Nova Zelândia)
Honório Serpa (Paraná, Brasil) e Naha (Okinawa, Japão)
Santa Vitória do Palmar (Rio Grande do Sul, Brasil) e Jeju-do (Coreia do Sul)
Barra do Quaraí (Rio Grande do Sul, Brasil) e Zhoushan (China)
Tramandaí (Rio Grande do Sul, Brasil) e Ilha Kuchinoshima (Kagoshima, Japão)
Osório (Rio Grande do Sul, Brasil) e Ilha Nakanoshima (Kagoshima, Japão)
Arganda del Rey (Espanha) e Taumatawhakatangihangakoauauotamateapokaiwhenuakitanatahu (Nova Zelândia)
Tangará da Serra, Vale de São Domingos, Conquista d'Oeste (Mato Grosso, Brasil); e Manila (Filipinas)
Altamira (Pará, Brasil) e Davao (Filipinas)
São Raimundo das Mangabeiras, Sambaíba, Loreto (Maranhão, Brasil), Ribeiro Gonçalves, Baixa Grande do Ribeiro (Piauí, Brasil); e Koror/Melequeoque/Angaur (Babeldaob, Palau)
Imperatriz (Maranhão, Brasil) e Ilhas Sonsorol (Palau)
Casa Nova, Remanso (Bahia, Brasil); e Colonia (Yap, Estados Federados da Micronésia)
Boa Vista (Roraima, Brasil) e Kajoeberang (Celebes Ocidental, Indonésia)
Plataforma do Urucu (Coari, Amazonas, Brasil) e Bandar Seri Begauã (Brunei)
Barcelos (Amazonas, Brasil) e Samarinda (Indonésia)
Tapauá (Amazonas, Brasil) e Kota Kinabalu (Sabá, Malásia)
Neiva (Colômbia) e Palimbão (Indonésia)
Estreito de Magalhães (Chile) e Lago Baical (Rússia)
Honolulu (Havaí, Estados Unidos) e Ghanzi (Botsuana)
Ilha de Páscoa (Chile) e Distrito de Jaisalmer (Rajastão, Índia)
Pequim (China) e Conesa (Rio Negro, Argentina)
Xangai (China) e Entre Ríos (Argentina)
Hong Kong (China) e Jujuy (Argentina)
Taipé (Taiwan) e Pilagás (Formosa, Argentina)
Singapura e Pastaza/Orellana (Equador)
Kuala Lumpur (Malásia) e Morona-Santiago (Equador)
Dubai (Emirados Árabes Unidos) e Ilha Ducie (Ilhas Pitcairn)
Jidá (Arábia Saudita) e Atol Tematangi (Tuamotu, Polinésia Francesa)
Cartum (Sudão) e proximidades do atol de Rangiroa (Tuamotu, Polinésia Francesa)
Gao (Mali) e Vanua Levu (Fiji)
Maradi (Níger) e Ilha de Savai'i (Samoa)
Tânger (Marrocos) e Whangarei (Nova Zelândia)
Condados de Toole, Liberty, Hill (Montana, Estados Unidos); Alberta, Saskatchewan (Canadá); e Ilhas Kerguelen (Terras Austrais e Antárticas Francesas)
Condado de Cheyenne (Colorado, Estados Unidos) e São Paulo (Terras Austrais e Antárticas Francesas)
Condado de Prowers (Colorado, Estados Unidos) e Île Amsterdam (Terras Austrais e Antárticas Francesas)
O Centro geográfico do Brasil, São José do Xingu, nordeste do Mato Grosso - latitude 10°20' Sul, longitude 53°12' Oeste, tem como antípoda o Mar das Filipinas, ficando, porém, bem próximo ao leste das Filipinas, na latitude de Cebu.
Boca do Acre (Amazonas, Brasil) e Ilha Spratly (Vietnã). Localizada no arquipélago de mesmo nome (Ilhas Spratly), a ilha é objeto de disputa territorial.

Generalização

Em matemática, o contender-se sobre uma esfera de qualquer dimensão $S^{n}$ : dois pontos à superfícies são antipodais se são opostos em relação ao centro.

O teorema de Borsuk-Ulam é um resultado da topologia algébrica que incide sobre estes pares de pontos. Afirma que uma qualquer função contínua de $S^{n}$ sobre $\mathbb {R} ^{n}$ transforma pelo menos um par de pontos antipodais de $S^{n}$ sobre o mesmo ponto de $\mathbb {R} ^{n}$ .

A função antipodal $A:S^{n}\rightarrow S^{n}$ definida por $A(x)=-x$ transforma todos os pontos de uma esfera no seu ponto antipodal. É assim homotópica à função identidade se $n$ é ímpar.