Bitangente
Em matemática, uma bitangente, ou tangente dupla, a uma curva C é uma linha L que toca C em dois pontos distintos P e Q e que tem a mesma direção que C nesses pontos. Ou seja, L é uma linha tangente em P e em Q.
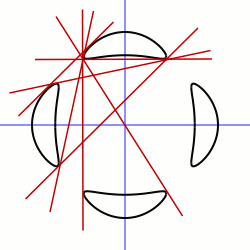
Bitangentes de curvas algébricas
editarEm geral, uma curva algébrica terá infinitas linhas secantes, mas apenas finitamente muitos bitangentes.
O teorema de Bézout implica que uma curva plana com um bitangente deve ter grau pelo menos 4. O caso dos 28 bitangentes de um quártico era uma peça célebre da geometria do século XIX, mostrando uma relação com as 27 linhas na superfície cúbica.
Bitangentes de polígonos
editarOs quatro bitangentes de dois polígonos convexos separados podem ser encontrados eficientemente por um algoritmo baseado na pesquisa binária, no qual se mantém um ponteiro de pesquisa binário nas listas de arestas de cada polígono e move um dos ponteiros para a esquerda ou para a direita em cada etapa, dependendo de onde as linhas tangentes às arestas dos dois ponteiros se cruzam. Esse cálculo da bitangente é uma sub-rotina essencial nas estruturas de dados para manter dinamicamente os cascos convexos (Overmars & van Leeuwen 1981). Pocchiola e Vegter (1996a, 1996b) descrevem um algoritmo para listar com eficiência todos os segmentos de linhas bitangentes que não cruzam nenhuma das outras curvas em um sistema de múltiplas curvas convexas disjuntas, usando uma técnica baseada em pseudotriangulação.
Bitangentes podem ser usados para acelerar a abordagem do gráfico de visibilidade para resolver o problema do caminho mais curto euclidiano: o caminho mais curto entre uma coleção de obstáculos poligonais só pode entrar ou sair do limite de um obstáculo ao longo de um de seus bitangentes, para que o caminho mais curto possa ser encontrado aplicando o algoritmo de Dijkstra a um subgráfico do gráfico de visibilidade formado pelas arestas de visibilidade que se encontram em linhas bitangentes (Rohnert 1986).
Conceitos relacionados
editarUm bitangente difere de uma linha secante, pois uma linha secante pode cruzar a curva nos dois pontos em que a cruza. Pode-se também considerar bitangentes que não são linhas; por exemplo, o conjunto de simetria de uma curva é o lugar geométrico dos centros de círculos tangentes à curva em dois pontos.
Bitangentes em pares de círculos figuram proeminentemente na construção dos círculos de Malfatti, em Jakob Steiner, em 1826, no problema do cinto de calcular o comprimento de um cinto conectando duas polias, no teorema de Casey caracterizando conjuntos de quatro círculos com um círculo tangente comum, e em O teorema de Monge sobre a colinearidade de pontos de interseção de certos bitangentes.
Referências
editar- Overmars, M. H.; van Leeuwen, J. (1981), «Maintenance of configurations in the plane», Journal of Computer and System Sciences, 23 (2), pp. 166–204, doi:10.1016/0022-0000(81)90012-X
- Pocchiola, Michel; Vegter, Gert (1996a), «The visibility complex», International Journal of Computational Geometry and Applications, 6 (3), pp. 297–308, doi:10.1142/S0218195996000204, Preliminary version in Ninth ACM Symposium on Computational Geometry (1993) 328–337]., consultado em 12 de abril de 2007, cópia arquivada em 3 de dezembro de 2006 .
- Pocchiola, Michel; Vegter, Gert (1996b), «Topologically sweeping visibility complexes via pseudotriangulations», Discrete and Computational Geometry, 16 (4), pp. 419–453, doi:10.1007/BF02712876 .
- Rohnert, H. (1986), «Shortest paths in the plane with convex polygonal obstacles», Information Processing Letters, 23 (2), pp. 71–76, doi:10.1016/0020-0190(86)90045-1