Lemniscata de Bernoulli

A Lemniscata de Bernoulli é a curva algébrica do quarto grau de equação cartesiana:

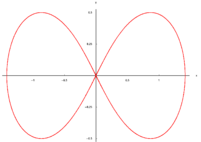
A Lemniscata de Bernoulli

$(x^{2}\ +\ y^{2})^{2}=a^{2}\ (x^{2}\ -\ y^{2})$

A lemniscata também pode ser descrita pelas coordenadas polares abaixo,

$r^{2}=a^{2}\cos 2\theta \,$

pelas respectivas coordenadas bipolares,

$rr'={\frac {a^{2}}{2}}$

ou pela equação paramétrica:

Coordenadas bipolares$x=a\cos t{\sqrt {2\cos(2t)}};\qquad y=a\sin t{\sqrt {2\cos(2t)}}$

A curva tem a forma similar ao numeral 8 e o símbolo de infinito ($\infty$).

A lemniscata foi descrita primeiramente por Jakob Bernoulli em 1694 como uma modificação da elipse, que é o lugar geométrico de pontos para qual a soma das distâncias para cada um de dois focos fixos é uma constante. A Oval de Cassini, por sua vez, é o lugar de pontos para os quais o produto destas distâncias é constante. No caso onde a curva atravessa o ponto no meio caminho entre os focos, a oval é uma lemniscata de Bernoulli.

Bernoulli chamou isto de lemniscus que em latim significa "faixa suspensa". A lemniscata pode ser obtida como o inverso geométrico de uma hipérbole, com o círculo de inversão centrado no centro da hipérbole (bissetriz de seus dois focos).

Derivadas

Cada derivada abaixo foi calculada usando derivações implícitas.

Com $y$ em função de $x$

${\frac {dy}{dx}}={\begin{cases}{\mbox{infinito}}&{\mbox{se }}y=0{\mbox{ e }}x\neq 0\\\pm 1&{\mbox{se }}y=0{\mbox{ e }}x=0\\{\frac {x(a^{2}-2x^{2}-2y^{2})}{y(a^{2}+2x^{2}+2y^{2})}}&{\mbox{se }}y\neq 0\end{cases}}$

${\frac {d^{2}y}{dx^{2}}}={\begin{cases}{\mbox{infinito}}&{\mbox{se }}y=0{\mbox{ e }}x\neq 0\\0&{\mbox{se }}y=0{\mbox{ e }}x=0\\{\frac {3a^{6}(y^{2}-x^{2})}{y^{3}(a^{2}+2x^{2}+2y^{2})^{3}}}&{\mbox{se }}y\neq 0\end{cases}}$

Com $x$ em função de $y$

${\frac {dx}{dy}}={\begin{cases}{\mbox{infinito}}&{\mbox{se }}2x^{2}+2y^{2}=a^{2}\\\pm 1&{\mbox{se }}x=0{\mbox{ e }}y=0\\{\frac {y(a^{2}+2x^{2}+2y^{2})}{x(a^{2}-2x^{2}-2y^{2})}}&{\mbox{caso contrario }}\end{cases}}$

${\frac {d^{2}x}{dy^{2}}}={\begin{cases}{\mbox{infinito}}&{\mbox{se }}2x^{2}+2y^{2}=a^{2}\\0&{\mbox{se }}x=0{\mbox{ e }}y=0\\{\frac {3a^{6}(x^{2}-y^{2})}{x^{3}(a^{2}-2x^{2}-2y^{2})^{3}}}&{\mbox{caso contrario }}\end{cases}}$

Curvatura

Quando as duas primeiras derivadas são conhecidas, a curvatura é facilmente calculada:

$\kappa =\pm 3(x^{2}+y^{2})^{1/2}a^{-2}\,$

O sinal a ser escolhido deve ser de acordo com a direção de movimento ao longo da curva. A lemniscata tem a propriedade da qual a magnitude da curvatura em qualquer ponto é proporcional à distância daquele ponto da origem.

Comprimento de arco como parâmetro e funções elípticas

A determinação do comprimento de arco como parâmetro da lemniscata levou às integrais elípticas, descobertas durante o século XVIII. Por volta de 1800, essa função elíptica era estudada por Carl Friedrich Gauss. Largamente inédito na ocasião, mas foram feitas insinuações a elas nas notas de sua obra "Disquisitiones Arithmeticae".

Seção

Lemniscata de Bernoulli em um torus secionado.

É possível obter a curva, secionando-se um torus por meio de um plano paralelo ao eixo de revolução. A tangência do perímetro interno origina uma Lemniscata no contorno da seção.

Ver também

• Lista de construções do desenho geométrico