Em teoria das probabilidades e estatística , a distribuição F de Fisher-Snedecor , também conhecida como distribuição F , distribuição F de Fisher e distribuição F de Snedecor , em homenagem ao biólogo e estatístico britânico Ronald Fisher e ao matemático norte-americano George Waddel Snedecor ,[ 1] distribuição de probabilidade contínua que surge frequentemente como a distribuição nula da estatística de um teste, mais notadamente na análise de variância , como no teste F .[ 2] [ 3] [ 4] [ 5]
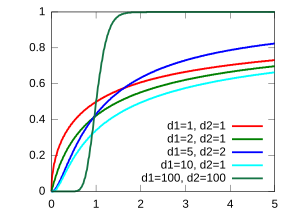
Função densidade de probabilidade
Função distribuição acumulada
Parâmetros
d
1
{\displaystyle d_{1}}
d
2
>
0
{\displaystyle d_{2}>0}
Suporte
x
∈
[
0
,
+
∞
)
{\displaystyle x\in [0,+\infty )}
f.d.p.
(
d
1
x
)
d
1
d
2
d
2
(
d
1
x
+
d
2
)
d
1
+
d
2
x
B
(
d
1
2
,
d
2
2
)
{\displaystyle {\frac {\sqrt {\frac {(d_{1}\,x)^{d_{1}}\,\,d_{2}^{d_{2}}}{(d_{1}\,x+d_{2})^{d_{1}+d_{2}}}}}{x\,\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\!}
f.d.a.
I
d
1
x
d
1
x
+
d
2
(
d
1
2
,
d
2
2
)
{\displaystyle I_{\frac {d_{1}x}{d_{1}x+d_{2}}}\left({\tfrac {d_{1}}{2}},{\tfrac {d_{2}}{2}}\right)}
Média
d
2
d
2
−
2
{\displaystyle {\frac {d_{2}}{d_{2}-2}}\!}
d
2
>
2
{\displaystyle d_{2}>2}
Moda
d
1
−
2
d
1
d
2
d
2
+
2
{\displaystyle {\frac {d_{1}-2}{d_{1}}}\;{\frac {d_{2}}{d_{2}+2}}}
d
1
>
2
{\displaystyle d_{1}>2}
Variância
2
d
2
2
(
d
1
+
d
2
−
2
)
d
1
(
d
2
−
2
)
2
(
d
2
−
4
)
{\displaystyle {\frac {2\,d_{2}^{2}\,(d_{1}+d_{2}-2)}{d_{1}(d_{2}-2)^{2}(d_{2}-4)}}\!}
d
2
>
4
{\displaystyle d_{2}>4}
Obliquidade
(
2
d
1
+
d
2
−
2
)
8
(
d
2
−
4
)
(
d
2
−
6
)
d
1
(
d
1
+
d
2
−
2
)
{\displaystyle {\frac {(2d_{1}+d_{2}-2){\sqrt {8(d_{2}-4)}}}{(d_{2}-6){\sqrt {d_{1}(d_{1}+d_{2}-2)}}}}\!}
d
2
>
6
{\displaystyle d_{2}>6}
Curtose Definida no texto.
Entropia
ln
(
σ
2
π
e
)
{\displaystyle \ln \left(\sigma {\sqrt {2\,\pi \,{\rm {e}}}}\right)\!~}
Função Geradora de Momentos Não existe. Os momentos brutos estão definidos no texto.
Função Característica
Γ
(
d
1
+
d
2
2
)
Γ
(
d
2
2
)
U
(
d
1
2
,
1
−
d
2
2
,
−
d
2
d
1
ı
t
)
{\displaystyle {\frac {\Gamma ({\frac {d_{1}+d_{2}}{2}})}{\Gamma ({\tfrac {d_{2}}{2}})}}U\!\left({\frac {d_{1}}{2}},1-{\frac {d_{2}}{2}},-{\frac {d_{2}}{d_{1}}}\imath t\right)}
U
(
a
,
b
,
z
)
{\displaystyle U(a,b,z)}
Se uma variável aleatória
X
{\displaystyle X}
F com parâmetros
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
X
∼
F
(
d
1
,
d
2
)
{\displaystyle X\sim F(d_{1},d_{2})}
função densidade de probabilidade de
X
{\displaystyle X}
f
(
x
;
d
1
,
d
2
)
=
(
d
1
x
)
d
1
d
2
d
2
(
d
1
x
+
d
2
)
d
1
+
d
2
x
B
(
d
1
2
,
d
2
2
)
=
1
B
(
d
1
2
,
d
2
2
)
(
d
1
d
2
)
d
1
2
x
d
1
2
−
1
(
1
+
d
1
d
2
x
)
−
d
1
+
d
2
2
{\displaystyle {\begin{aligned}f(x;d_{1},d_{2})&={\frac {\sqrt {\frac {(d_{1}\,x)^{d_{1}}\,\,d_{2}^{d_{2}}}{(d_{1}\,x+d_{2})^{d_{1}+d_{2}}}}}{x\,\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\\&={\frac {1}{\mathrm {B} \!\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\left({\frac {d_{1}}{d_{2}}}\right)^{\frac {d_{1}}{2}}x^{{\frac {d_{1}}{2}}-1}\left(1+{\frac {d_{1}}{d_{2}}}\,x\right)^{-{\frac {d_{1}+d_{2}}{2}}}\end{aligned}}}
para
x
{\displaystyle x}
real e maior que zero. Aqui,
B
{\displaystyle \mathrm {B} }
função beta . Em muitas aplicações, os parâmetros
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
inteiros positivos , mas a distribuição é bem definida para valores reais positivos destes parâmetros.
A função distribuição acumulada é
F
(
x
;
d
1
,
d
2
)
=
I
d
1
x
d
1
x
+
d
2
(
d
1
2
,
d
2
2
)
,
{\displaystyle F(x;d_{1},d_{2})=I_{\frac {d_{1}x}{d_{1}x+d_{2}}}\left({\tfrac {d_{1}}{2}},{\tfrac {d_{2}}{2}}\right),}
em que
I
{\displaystyle I}
O valor esperado , a variância e outros detalhes sobre
F
(
d
1
,
d
2
)
{\displaystyle F(d_{1},d_{2})}
d
2
>
8
{\displaystyle d_{2}>8}
curtose de excesso é
γ
2
=
12
d
1
(
5
d
2
−
22
)
(
d
1
+
d
2
−
2
)
+
(
d
2
−
4
)
(
d
2
−
2
)
2
d
1
(
d
2
−
6
)
(
d
2
−
8
)
(
d
1
+
d
2
−
2
)
{\displaystyle \gamma _{2}=12{\frac {d_{1}(5d_{2}-22)(d_{1}+d_{2}-2)+(d_{2}-4)(d_{2}-2)^{2}}{d_{1}(d_{2}-6)(d_{2}-8)(d_{1}+d_{2}-2)}}}
O
k
{\displaystyle k}
F
(
d
1
,
d
2
)
{\displaystyle F(d_{1},d_{2})}
2
k
<
d
2
{\displaystyle 2k<d_{2}}
[ 6]
μ
X
(
k
)
=
(
d
2
d
1
)
k
Γ
(
d
1
2
+
k
)
Γ
(
d
1
2
)
Γ
(
d
2
2
−
k
)
Γ
(
d
2
2
)
{\displaystyle \mu _{X}(k)=\left({\frac {d_{2}}{d_{1}}}\right)^{k}{\frac {\Gamma \left({\tfrac {d_{1}}{2}}+k\right)}{\Gamma \left({\tfrac {d_{1}}{2}}\right)}}{\frac {\Gamma \left({\tfrac {d_{2}}{2}}-k\right)}{\Gamma \left({\tfrac {d_{2}}{2}}\right)}}}
A distribuição F é uma parametrização particular da distribuição beta prima, também chamada de distribuição beta de segundo tipo.
A função característica é[ 7]
φ
d
1
,
d
2
F
(
s
)
=
Γ
(
d
1
+
d
2
2
)
Γ
(
d
2
2
)
U
(
d
1
2
,
1
−
d
2
2
,
−
d
2
d
1
ı
s
)
{\displaystyle \varphi _{d_{1},d_{2}}^{F}(s)={\frac {\Gamma ({\frac {d_{1}+d_{2}}{2}})}{\Gamma ({\tfrac {d_{2}}{2}})}}U\!\left({\frac {d_{1}}{2}},1-{\frac {d_{2}}{2}},-{\frac {d_{2}}{d_{1}}}\imath s\right)}
em que
U
(
a
,
b
,
z
)
{\displaystyle U(a,b,z)}
O valor observado de uma variável aleatória de distribuição F com parâmetros
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
[ 8]
X
=
U
1
/
d
1
U
2
/
d
2
{\displaystyle X={\frac {U_{1}/d_{1}}{U_{2}/d_{2}}}}
em que
U
1
{\displaystyle U_{1}}
U
2
{\displaystyle U_{2}}
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
U
1
{\displaystyle U_{1}}
U
2
{\displaystyle U_{2}}
independentes .Em instâncias em que a distribuição F é usada, por exemplo, na análise de variância, a independência de
U
1
{\displaystyle U_{1}}
U
2
{\displaystyle U_{2}}
Equivalentemente, a variável aleatória da distribuição F também pode ser escrita como
X
=
s
1
2
σ
1
2
/
s
2
2
σ
2
2
{\displaystyle X={\frac {s_{1}^{2}}{\sigma _{1}^{2}}}\;/\;{\frac {s_{2}^{2}}{\sigma _{2}^{2}}}}
em que
s
1
2
{\displaystyle s_{1}^{2}}
s
2
2
{\displaystyle s_{2}^{2}}
S
1
2
{\displaystyle S_{1}^{2}}
S
2
2
{\displaystyle S_{2}^{2}}
σ
1
2
{\displaystyle \sigma _{1}^{2}}
σ
2
2
{\displaystyle \sigma _{2}^{2}}
χ
2
{\displaystyle \chi ^{2}}
d
1
{\displaystyle d_{1}}
d
2
{\displaystyle d_{2}}
s
1
2
=
S
1
2
d
1
{\displaystyle s_{1}^{2}={\frac {S_{1}^{2}}{d_{1}}}}
s
2
2
=
S
2
2
d
2
{\displaystyle s_{2}^{2}={\frac {S_{2}^{2}}{d_{2}}}}
Em um contexto frequencista , uma distribuição F escalada dá portanto a probabilidade
p
(
s
1
2
/
s
2
2
|
σ
1
2
,
σ
2
2
)
{\displaystyle p(s_{1}^{2}/s_{2}^{2}|\sigma _{1}^{2},\sigma _{2}^{2})}
σ
1
2
{\displaystyle \sigma _{1}^{2}}
σ
2
2
{\displaystyle \sigma _{2}^{2}}
F aparece de forma mais generalizada em testes F : em que a hipótese nula é de que duas variâncias normais independentes são iguais e as somas observadas de alguns quadrados apropriadamente selecionados são então examinadas a fim de verificar se sua razão é significantemente incompatível com esta hipótese nula.
A quantidade
X
{\displaystyle X}
bayesiana , se um método de Jeffreys não informativo, de rescalamento invariante for tomado para as probabilidades a priori de
σ
1
2
{\displaystyle \sigma _{1}^{2}}
σ
2
2
{\displaystyle \sigma _{2}^{2}}
[ 9] F escalada dá assim a probabilidade a posteriori
p
(
σ
1
2
,
σ
2
2
|
s
1
2
/
s
2
2
)
{\displaystyle p(\sigma _{1}^{2},\sigma _{2}^{2}|s_{1}^{2}/s_{2}^{2})}
s
1
2
{\displaystyle s_{1}^{2}}
s
2
2
{\displaystyle s_{2}^{2}}
De forma geral, resumida e simplificada, a distribuição F tem como características básicas:
É uma família de curvas, cada uma, determinada por dois tipos de graus de liberdade, os correspondentes à variância no numerador, e os que correspondem à variância no denominador.
É uma distribuição positivamente assimétrica.
A área total sob cada curva de uma distribuição F é igual a 1.
Todos os valores de X são maiores ou iguais a 0.
Para todas as distribuições F, o valor médio de X é aproximadamente igual a 1.[ 10] A função densidade de probabilidade da distribuição F é uma solução da seguinte equação diferencial :
{
2
x
(
d
1
x
+
d
2
)
f
′
(
x
)
+
(
2
d
1
x
+
d
2
d
1
x
−
d
2
d
1
+
2
d
2
)
f
(
x
)
=
0
,
f
(
1
)
=
d
1
d
1
2
d
2
d
2
2
(
d
1
+
d
2
)
1
2
(
−
d
1
−
d
2
)
B
(
d
1
2
,
d
2
2
)
}
{\displaystyle \left\{{\begin{array}{l}2x\left(d_{1}x+d_{2}\right)f'(x)+\left(2d_{1}x+d_{2}d_{1}x-d_{2}d_{1}+2d_{2}\right)f(x)=0,\\[12pt]f(1)={\frac {d_{1}^{\frac {d_{1}}{2}}d_{2}^{\frac {d_{2}}{2}}\left(d_{1}+d_{2}\right){}^{{\frac {1}{2}}\left(-d_{1}-d_{2}\right)}}{B\left({\frac {d_{1}}{2}},{\frac {d_{2}}{2}}\right)}}\end{array}}\right\}}
editar
Se
X
∼
χ
d
1
2
{\displaystyle X\sim \chi _{d_{1}}^{2}}
Y
∼
χ
d
2
2
{\displaystyle Y\sim \chi _{d_{2}}^{2}}
X
/
d
1
Y
/
d
2
∼
F
(
d
1
,
d
2
)
{\displaystyle {\frac {X/d_{1}}{Y/d_{2}}}\sim \mathrm {F} (d_{1},d_{2})}
Se
X
k
∼
Γ
(
α
k
,
β
k
)
{\displaystyle X_{k}\sim \Gamma (\alpha _{k},\beta _{k})\,}
α
2
β
1
X
1
α
1
β
2
X
2
∼
F
(
2
α
1
,
2
α
2
)
{\displaystyle {\frac {\alpha _{2}\beta _{1}X_{1}}{\alpha _{1}\beta _{2}X_{2}}}\sim \mathrm {F} (2\alpha _{1},2\alpha _{2})}
Se
X
∼
Beta
(
d
1
/
2
,
d
2
/
2
)
{\displaystyle X\sim \operatorname {Beta} (d_{1}/2,d_{2}/2)}
d
2
X
d
1
(
1
−
X
)
∼
F
(
d
1
,
d
2
)
{\displaystyle {\frac {d_{2}X}{d_{1}(1-X)}}\sim \operatorname {F} (d_{1},d_{2})}
Equivalentemente, se
X
∼
F
(
d
1
,
d
2
)
{\displaystyle X\sim F(d_{1},d_{2})}
d
1
X
/
d
2
1
+
d
1
X
/
d
2
∼
Beta
(
d
1
/
2
,
d
2
/
2
)
{\displaystyle {\frac {d_{1}X/d_{2}}{1+d_{1}X/d_{2}}}\sim \operatorname {Beta} (d_{1}/2,d_{2}/2)}
Se
X
∼
F
(
d
1
,
d
2
)
{\displaystyle X\sim F(d_{1},d_{2})}
Y
=
lim
d
2
→
∞
d
1
X
{\displaystyle Y=\lim _{d_{2}\to \infty }d_{1}X}
distribuição qui-quadrado
χ
d
1
2
{\displaystyle \chi _{d_{1}}^{2}}
F
(
d
1
,
d
2
)
{\displaystyle F(d_{1},d_{2})}
d
2
d
1
(
d
1
+
d
2
−
1
)
T
2
(
d
1
,
d
1
+
d
2
−
1
)
{\displaystyle {\frac {d_{2}}{d_{1}(d_{1}+d_{2}-1)}}\operatorname {T} ^{2}(d_{1},d_{1}+d_{2}-1)}
Se
X
∼
F
(
d
1
,
d
2
)
{\displaystyle X\sim F(d_{1},d_{2})}
X
−
1
∼
F
(
d
2
,
d
1
)
{\displaystyle X^{-1}\sim F(d_{2},d_{1})}
Se
X
∼
t
(
n
)
{\displaystyle X\sim t(n)}
distribuição t de Student ), então:
X
2
∼
F
(
1
,
n
)
{\displaystyle X^{2}\sim \operatorname {F} (1,n)}
X
−
2
∼
F
(
n
,
1
)
{\displaystyle X^{-2}\sim \operatorname {F} (n,1)}
A distribuição F é um caso especial de distribuição de Pearson de tipo 6;
Se
X
{\displaystyle X}
Y
{\displaystyle Y}
X
,
Y
∼
L
a
p
l
a
c
e
(
μ
,
b
)
{\displaystyle X,Y\sim \mathrm {Laplace} (\mu ,b)}
|
X
−
μ
|
|
Y
−
μ
|
∼
F
(
2
,
2
)
{\displaystyle {\tfrac {|X-\mu |}{|Y-\mu |}}\sim \operatorname {F} (2,2)}
Se
X
∼
F
(
n
,
m
)
{\displaystyle X\sim F(n,m)}
log
X
2
∼
FisherZ
(
n
,
m
)
{\displaystyle {\frac {\log {X}}{2}}\sim \operatorname {FisherZ} (n,m)}
A distribuição F não central simplifica à distribuição F se
λ
=
0
{\displaystyle \lambda =0}
A distribuição F não central dupla simplifica à distribuição F se
λ
1
=
λ
2
=
0
{\displaystyle \lambda _{1}=\lambda _{2}=0}
Se
Q
X
(
p
)
{\displaystyle \operatorname {Q} _{X}(p)}
p
{\displaystyle p}
X
∼
F
(
d
1
,
d
2
)
{\displaystyle X\sim F(d_{1},d_{2})}
Q
Y
(
1
−
p
)
{\displaystyle \operatorname {Q} _{Y}(1-p)}
1
−
p
{\displaystyle 1-p}
Y
∼
F
(
d
2
,
d
1
)
{\displaystyle Y\sim F(d_{2},d_{1})}
Q
X
(
p
)
=
1
Q
Y
(
1
−
p
)
{\displaystyle \operatorname {Q} _{X}(p)={\frac {1}{\operatorname {Q} _{Y}(1-p)}}}
↑ «Earliest Known Uses of Some of the Words of Mathematics (F)» . jeff560.tripod.com . Consultado em 19 de junho de 2017 ↑ Johnson, Norman Lloyd; Kotz, Samuel; Balakrishnan, N. (8 de maio de 1995). Continuous univariate distributions ISBN 9780471584940 ↑ Abramowitz, Milton; Stegun, Irene A. (30 de abril de 2012). Handbook of Mathematical Functions: with Formulas, Graphs, and Mathematical Tables ISBN 9780486158242 ↑ «1.3.6.6.5. F Distribution» . www.itl.nist.gov . Consultado em 19 de junho de 2017 ↑ Mood, Alexander McFarlane; Graybill, Franklin A.; Boes, Duane C. (janeiro 1974). Introduction to the Theory of Statistics ISBN 9780070428645 ↑ «F distribution» . www.statlect.com . Consultado em 19 de junho de 2017 ↑ Phillips, P. C. B. (1 de abril de 1982). «The true characteristic function of the F distribution» . Biometrika . 69 (1): 261–264. ISSN 0006-3444 . doi :10.1093/biomet/69.1.261 ↑ DeGroot, Morris H.; Schervish, Mark J. (2002). Probability and Statistics ISBN 9780201524888 ↑ Box, George E. P.; Tiao, George C. (25 de janeiro de 2011). Bayesian Inference in Statistical Analysis ISBN 9781118031445 ↑ LARSON, Ron; FARBER, Betsy (2016). Estatística Aplicada . São Paulo: PEARSON. 2 páginas