Distribuição uniforme

Em estatística e probabilidade, a distribuição uniforme é a distribuição de probabilidades contínua mais simples de conceituar: a probabilidade de se gerar qualquer ponto em um intervalo contido no espaço amostral é proporcional ao tamanho do intervalo, visto que na distribuição uniforme a f(x) é igual para qualquer valor de x no intervalo considerado. Por exemplo, se considerarmos um intervalo em x de zero à dez positivo (xЄ[0,10] ), e assumirmos que temos uma distribuição uniforme nesse intervalo, a probabilidade de f(x) no intervalo  2<x<5 é igual a probabilidade de f(x) no intervalo  5<x<8 pois sabemos que a distribuição é uniforme nesses intervalos e possuímos os intervalos com o mesmo tamanho.

A função densidade da distribuição uniforme em [a,b].

Outra maneira de se dizer "distribuição uniforme" seria "um número finito de resultados com chances iguais de acontecer".

Ela é usada quando assumimos intervalos iguais da variável que a mesma probabilidade .

Um simples exemplo de distribuição uniforme é lançar um dado não viciado. Os possíveis valores são 1,2,3,4,5,6, e a cada turno que o dado é jogado a probabilidade de cada valor é 1/6. Se dois dados são lançados e seus valores adicionados, a distribuição resultante não é mais uniforme pois as somas não são uma variável equiprovável.

A distribuição discreta uniforme em si não possui parâmetros. No entanto, é conveniente representar seus possíveis resultados com um intervalo fechado [a,b], sendo 'a' e 'b' considerados os principais parâmetros da distribuição. Com isso a função acumulada dessa distribuição é representada como:

$F(x)=P(X\leq x)=\int \limits _{-\infty }^{x}f(x)dx=\left\{{\begin{array}{ccl}0,&{\text{se}}&x<\alpha \\{\frac {x-\alpha }{\beta -\alpha }},&{\text{se}}&\alpha \leq x<\beta \\1,&{\text{se}}&x\geq \beta \end{array}}\right.$

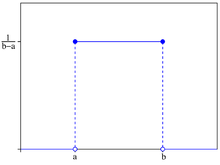
Seja [a,b] o espaço amostral. Então temos que a função densidade de probabilidade é:

Em linguagem matemática	Em Português
$f(x;a,b)=\left\{{\begin{matrix}{\color {Red}{\frac {1}{b-a}}}&,\;a\leq x\leq b,\\0&,\;c.c.\end{matrix}}\right.$	A probabilidade de a variável aleatória X ocorrer no intervalo infinitesimal [x*, x*+dx] é ${\color {Red}{\frac {dx}{b-a}}}$ se x estiver entre a e b, e zero em caso contrário.

Esta distribuição tem valor médio ou esperança matemática de X, dada por $E(X)={\frac {a+b}{2}}\,$ e variância $Var(X)={\frac {(b-a)^{2}}{12}}\,$.

Exemplo básico:

1) Um ponto é escolhido ao acaso no intervalo $[0,2]$. Qual será a probabilidade de que o ponto escolhido esteja entre $1$ e $3/2$?

A sua função de distribuição acumulada é dada por:

$F(x)=\left\{{\begin{array}{ccl}{\frac {1}{2}},&{\text{se}}&x\in [0,2]\\0,&{\text{caso contrário}}\end{array}}\right.$

Portanto,

$P(1\leq x\leq 3/2)={\frac {[(3/2)-1]}{(2-0)}}={\frac {1/2}{2}}=0,25.$

Esperança e Variância: origem das fórmulas

A seguir, apresenta-se o desenvolvimento dos cálculos visando chegar as fórmulas anteriormente apresentadas, da esperança e por conseguinte da variância.

Seja X a variável com distribuição uniforme contínua no intervalo de “a” até “b”. Então:

$f(x)={1 \over b-a},a\leq x\leq b$

$f(x)=0$, caso contrário.

Aplicando a fórmula da esperança:

$E(X)=\int \limits _{-\infty }^{\infty }x\times f(x)dx$

$E(X)=\int \limits _{a}^{b}x\times {1 \over b-a}dx$

$E(X)={1 \over b-a}\left({\frac {x^{2}}{2}}\right)_{a}^{b}$

$E(X)={1 \over b-a}\times {b^{2}-a^{2} \over 2}$

Fatorando:

$E(X)={1 \over b-a}\times {(b-a)\times (b+a) \over 2}={b+a \over 2}$

Calculando a média de X²:

$E(X^{2})=\int \limits _{-\infty }^{\infty }x^{2}\times f(x)dx$

$E(X^{2})=\int \limits _{a}^{b}x^{2}\times {1 \over b-a}dx$

$E(X^{2})={1 \over b-a}\left({\frac {x^{3}}{3}}\right)_{a}^{b}$

$E(X^{2})={1 \over b-a}\times {b^{3}-a^{3} \over 3}$

Fatorando:

$E(X^{2})={1 \over b-a}\times {(b-a)\times (b^{2}+ab+a^{2}) \over 3}={b^{2}+ab+a^{2} \over 3}$

A fórmula da variância para a distribuição uniforme é a diferença entre a esperança de $X^{2}$ o quadrado da esperança de $X$. Então:

$Var(X)=E(X^{2})-E(X)^{2}$

$Var(X)={b^{2}+ab+a^{2} \over 3}-\left({\frac {b+a}{2}}\right)^{2}$

$Var(X)={b^{2}+ab+a^{2} \over 3}-{b^{2}+2ab+a^{2} \over 4}$

Tirando o mínimo múltiplo comum:

$Var(X)={4b^{2}+4ab+4a^{2} \over 12}-{3b^{2}+6ab+3a^{2} \over 12}$

$Var(X)={b^{2}-2ab+a^{2} \over 12}$

que nos dá a fórmula:

$Var(X)={(b-a)^{2} \over 12}$

Exemplos básicos

1) Considere uma experiência aleatória associada a 5 acontecimentos elementares ωi (i = 1, 2, 3, 4, 5) com as seguintes probabilidades:

i $\{$ 1 2 3 4 5

 ωi $\{$ 0 1 2 3 4

P(ωi) $\{$ 0.1 0.2 0.3 0.3 0.1

 Considere a variável aleatória, definida à custa dos acontecimentos elementares,

 $\{$2ωi , ωi ≥ 2

 X(ωi) =

                $\{$ 6ωi −8 , ωi < 2

Determine o valor esperado de X e a probabilidade de X assumir um valor negativo.

Solução:

E (X )= 2.6; P (X < 0)= 0.3

Propriedades da Distribuição Uniforme

As principais medidas para a distribuição uniforme podem ser determinadas de uma forma geral em termos dos extremos "a" e o "b" do intervalo.

Média, expectância ou valor esperado

$\mu =E(X)=\int \limits _{-\infty }^{\infty }x.f(x)dx=\int _{a}^{b}x.{\frac {1}{b-a}}dx=(a+b)/2$

Desvio Padrão

$\sigma =\surd {\frac {(b-a)^{2}}{12}}$

A FDA da distribuição Uniforme

A FDA da distribuição uniforme, pode ser facilmente avaliada e, vale:

$F(x)=P(X\leq x)=\int \limits _{-\infty }^{x}{\frac {1}{b-a}}du={\begin{cases}0,\qquad se\,x<a\\{\frac {x-a}{b-a}},\qquad se\ a\leq x\leq b\\1,\qquad se\ x>b\end{cases}}$

Exemplo:

Seja X uma VAC com distribuição uniforme no intervalo [5, 10]. Determinar as probabilidades:

a) P(X < 7)

b) P(X > 8,5)

c) P(8 < x < 9)

Soluções:

Utilizando a FDA da variável vem:

a) $P(X<7)=F(7){\binom {7-5}{10-5}}={\frac {2}{5}}=40\%$

b) $P(X>8,5)=1-P(X<8,5)=1-F(8,5)=1-{\binom {8,5-5}{10-5}}=1-{\frac {3,5}{5}}=1-0,7=30\%$

c) $P(8<X<9)=F(9)-F(8)={\frac {4}{5}}-{\frac {3}{5}}={\frac {1}{5}}=20\%$

Estimativa do máximo

Ver artigo principal: Problema dos tanques alemães

Esse exemplo é descrito com uma amostra de k observações obtidas de uma distribuição uniforme no inteiros $1,2,\dots ,N$, com o problema de se estimar o N máximo. Esse problema é comumente como o Problema dos tanques alemães.

O estimador de variancia mínima não-enviesada para o máximo é dado por

${\hat {N}}={\frac {k+1}{k}}m-1=m+{\frac {m}{k}}-1$

onde m é o maior valor da amostragem e k é o tamanho da amostra, sendo a amostragem sem reposição.

A fórmula pode ser entendida como:

"O valor máximo da amostra mais a média intervalar entre as observações na amostra".

Isto possui variância de

${\frac {1}{k}}{\frac {(N-k)(N+1)}{(k+2)}}\approx {\frac {N^{2}}{k^{2}}}{\text{ para amostras pequenas }}k\ll N$

Aplicações

Geral

No geral o uso de distribuição uniforme é utilizado para se ter o número das chances possíveis de um determinado evento ocorrer, dentro de um limite de duas variáveis logicas. Como por exemplo a probabilidade de peças com defeitos em um lote com determinada quantidade de peças.

Informática

A maioria das linguagens de programação, pacotes estatísticos ou planilhas de cálculo possuem um gerador de números aleatórios, que gera a partir de uma distribuição uniforme, com valores entre 0 e 1. Esse número é chamado de pseudo-aleatório, porque é possível repetir a mesma sequência a partir de uma mesma semente (valor inteiro).

Simulação de outras distribuições

Qualquer outra distribuição contínua, na qual a função distribuição acumulada seja invertível, pode ser simulada a partir da distribuição uniforme.

Seja U a distribuição uniforme com valores no intervalo [0,1], e X uma variável aleatória contínua com distribuição acumulada F(x). Então:

$X\sim F^{-1}(U)\,$

Para demonstrar, devemos provar que a chance de simular um valor de X entre a e b por esse método é igual à probabilidade da variável aleatória X gerar um valor entre a e b.

Por um lado, a chance de $F^{-1}(U)\in \left[a,b\right]\,$ é igual à chance de $U\in \left[F(a),F(b)\right]\,$ (pela monotonicidade de F), e, como $0\leq F(a)\leq F(b)\leq 1\,$, essa chance é igual a F(b)-F(a).

Por outro lado, a chance de X gerar um valor entre a e b, é a chance de X gerar um valor menor ou igual a b menos a chance de X gerar um valor menor ou igual a a (onde usamos o fato de X ser contínua, ou seja, a probabilidade um ponto é zero). Usando a definição de distribuição acumulada, essa chance é F(b)-F(a).

Erro de quantização

Numa conversão de valores analógicos para valores digitais, pode´se existir um erro baseado no arredondamento ou truncamento. Quando o erro é muito maior que um BIt menos significativo, o erro de quantização tem uma distribuição praticamente uniforme.

Veja também

• Função exponencial
• Delta de Dirac

Ligações externas

• «Calculadora - Distribuição uniforme»