Funções trigonométricas inversas

As funções trigonométricas inversas são as inversas de restrições apropriadas (restrições principais) das funções trigonométricas, usualmente são chamadas de função de arco pois retornam o arco correspondente a certa função trigonométrica.

Arcotangente.

Arcossecante e arcocossecante.

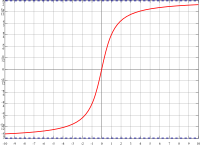
Nome	Notação 1	Notação 2	Definição	Domínio como função real	Imagem (em radianos)
arco seno	y = arcsen(x)	y = sen-1(x)	x = sen(y)	[−1,+1]	−π/2 ≤ y ≤ π/2
arco cosseno	y = arccos(x)	y = cos-1(x)	x = cos(y)	[−1,+1]	0 ≤ y ≤ π
arco tangente	y = arctg(x)	y = tg-1(x)	x = tg(y)	R	−π/2 < y < π/2
arco cotangente	y = arccot(x)	y = cot-1(x)	x = cotg(y)	R	0 < y < π
arco secante	y = arcsec(x)	y = sec-1(x)	x = sec(y)	[1,+∞[ ou ]−∞,-1]	0 ≤ y < π/2 ou π/2 < y ≤ π
arco cossecante	y = arccosec(x)	y = cosec-1(x)	x = cosec(y)	]−∞,−1] ou [1,+∞[	−π/2 ≤ y < 0 ou 0 < y ≤ π/2

Identidades

Algumas equações envolvendo funções trigonométricas inversas são importantes em uma série de aplicações e por isso recebem o nome de identidades. Exemplos são:

${\text{arc sen }}x+{\text{arc cos x}}={\frac {\pi }{2}}$

$\cos({\text{arc sen }}x)={\sqrt {1-x^{2}}}$

${\text{sen }}({\text{arc cos}}x)={\sqrt {1-x^{2}}}$

${\text{tg }}({\text{arc sen }}x)={\frac {x}{\sqrt {1-x^{2}}}}$

$\sec({\text{arc tg }}x)={\sqrt {1+x^{2}}}$

Essas identidades podem ser obtidas usando de relações trigonométricas fundamentais em triângulos retângulos.