Usando-se as expressões
sen
z
=
e
i
z
−
e
−
i
z
2
i
{\displaystyle \operatorname {sen} z={\frac {e^{iz}-e^{-iz}}{2i}}}
cos
z
=
e
i
z
+
e
−
i
z
2
{\displaystyle \cos z={\frac {e^{iz}+e^{-iz}}{2}}}
D
n
(
x
)
=
1
2
L
(
∑
k
=
−
n
n
e
k
π
i
x
L
)
{\displaystyle D_{n}(x)={\frac {1}{2L}}\left(\sum _{k=-n}^{n}e^{\frac {k\pi ix}{L}}\right)}
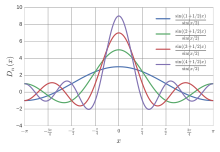
Esboço de
D
n
(
x
)
{\displaystyle D_{n}(x)}
x
∈
[
−
L
,
L
]
{\displaystyle x\in [-L,L]}
delta de Dirac .
D
n
(
x
)
{\displaystyle D_{n}(x)}
D
n
(
x
)
{\displaystyle D_{n}(x)}
função contínua ;
D
n
(
x
)
{\displaystyle D_{n}(x)}
∫
−
L
L
D
n
(
x
)
d
x
=
1
{\displaystyle \int _{-L}^{L}D_{n}(x)\ dx=1}
D
n
(
0
)
=
2
n
+
1
2
L
{\displaystyle D_{n}(0)={\frac {2n+1}{2L}}}
D
n
(
x
)
=
1
2
L
sen
(
n
+
1
2
)
π
x
L
sen
π
x
2
L
{\displaystyle D_{n}(x)={\frac {1}{2L}}{\frac {\operatorname {sen} \left(n+{\frac {1}{2}}\right){\frac {\pi x}{L}}}{\operatorname {sen} {\frac {\pi x}{2L}}}}}
x
≠
0
,
±
2
L
,
±
4
L
,
.
.
.
{\displaystyle x\neq 0,\pm 2L,\pm 4L,...}
editar
A identidade trigonométrica
∑
k
=
−
n
n
e
i
k
π
x
L
=
sen
(
(
n
+
1
/
2
)
π
x
L
)
sen
(
π
x
2
L
)
{\displaystyle \sum _{k=-n}^{n}e^{\frac {ik\pi x}{L}}={\frac {\operatorname {sen}((n+1/2){\frac {\pi x}{L}})}{\operatorname {sen}({\frac {\pi x}{2L}})}}}
A fórmula para a soma de termos em progressão geométrica é dada por:
∑
k
=
0
n
a
r
k
=
a
1
−
r
n
+
1
1
−
r
.
{\displaystyle \sum _{k=0}^{n}ar^{k}=a{\frac {1-r^{n+1}}{1-r}}.}
Em particular, tem-se:
∑
k
=
−
n
n
r
k
=
r
−
n
⋅
1
−
r
2
n
+
1
1
−
r
.
{\displaystyle \sum _{k=-n}^{n}r^{k}=r^{-n}\cdot {\frac {1-r^{2n+1}}{1-r}}.}
Multiplicando tanto o numerador como o denominador por
r
−
1
2
{\displaystyle r^{-{\frac {1}{2}}}}
r
−
n
−
1
/
2
r
−
1
/
2
⋅
1
−
r
2
n
+
1
1
−
r
=
r
−
n
−
1
/
2
−
r
n
+
1
/
2
r
−
1
/
2
−
r
1
/
2
.
{\displaystyle {\frac {r^{-n-1/2}}{r^{-1/2}}}\cdot {\frac {1-r^{2n+1}}{1-r}}={\frac {r^{-n-1/2}-r^{n+1/2}}{r^{-1/2}-r^{1/2}}}.}
No caso
r
=
e
i
π
x
L
{\textstyle r=e^{\frac {i\pi x}{L}}}
∑
k
=
−
n
n
e
i
k
π
x
L
=
e
−
(
n
+
1
/
2
)
i
π
x
L
−
e
(
n
+
1
/
2
)
i
π
x
L
e
−
i
π
x
2
L
−
e
i
π
x
2
L
=
−
2
i
sen
(
(
n
+
1
/
2
)
x
)
−
2
i
sen
(
x
/
2
)
=
sen
(
(
n
+
1
/
2
)
π
x
L
)
sen
(
π
x
2
L
)
{\displaystyle \sum _{k=-n}^{n}e^{\frac {ik\pi x}{L}}={\frac {e^{-(n+1/2){\frac {i\pi x}{L}}}-e^{(n+1/2){\frac {i\pi x}{L}}}}{e^{-{\frac {i\pi x}{2L}}}-e^{\frac {i\pi x}{2L}}}}={\frac {-2i\operatorname {sen}((n+1/2)x)}{-2i\operatorname {sen}(x/2)}}={\frac {\operatorname {sen}((n+1/2){\frac {\pi x}{L}})}{\operatorname {sen}({\frac {\pi x}{2L}})}}}
↑ Figueiredo, Djairo Guedes de (1997). Análise de Fourier e Equações Diferenciais Parciais Terceira ed. Rio de Janeiro: Projeto Euclides. p. 54-55. ISBN 85-244-0026-9