Oscilador de cristal
Um oscilador de cristal é um componente eletrônico que utiliza a ressonância de um cristal em vibração de um material piezoeletrônico, para criar um sinal elétrico com uma frequência bastante precisa. Esta frequência é comumente usada para medir precisamente o tempo, tais como em relógios de quartzo, bem como para estabilizar frequências de transmissores de rádio. O cristal piezoelétrico mais utilizado é quartzo.[1]
| Oscilador de cristal | |
|---|---|
| Oscilador de quartzo de 16MHz em encapsulamento HC-49/S | |
| Nome do componente | Oscilador de cristal |
| Princípio de funcionamento | Piezoeletricidade, Ressonância |
| Informações históricas | |
| Inventado por | Alexander M. Nicholson, Walter Guyton Cady |
| Primeira produção | 1956 |
| Uso | |
| Símbolo | 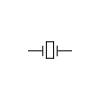
|
| Portal da Eletrônica | |
Osciladores de cristais são componentes compostos de dois terminais, ligados a um cristal piezoeléctrico interno.[2] Esse cristal contrai quando submetido a tensão elétrica, e o tempo de contração varia conforme a construção do cristal. Quando a contração chega a um certo ponto, o circuito libera a tensão e o cristal relaxa, chegando ao ponto de uma nova contração. Assim, os tempos de contração e relaxação desse ciclo determinam uma frequência de operação, muito mais estável e controlável que circuitos com capacitores. Cristais de quartzo são usados sobretudo em microcontroladores eletrônicos.[3]
Definição
editarOscilador de Cristal é um componente eletrônico que gera um sinal elétrico em uma frequência específica, através das propriedades piezoelétricas do cristal. O tipo de material mais comum é o cristal de quartzo. Logo, os circuitos que o utilizam são chamados de osciladores de quartzo, mas outros materiais podem ser usados com o mesmo propósito, como cerâmicas policristalinas.[2]
Histórico
editarA propriedade piezoelétrica foi descoberta em 1880 por Jacques Curie e Pierre Curie. Durante a Primeira Guerra Mundial Paul Langevin pesquisou o uso de ressonadores de quartzo para sonares.
O oscilador de cristal foi criado na década de 1920. Existem divergências a respeito dos pioneiros do desenvolvimento de quartzo como osciladores, que envolve diversos pesquisadores Walter Guyton Cady construiu os primeiros modelos em 1921, que disputava a prioridade da invenção com Alexander M Nicholson, que patenteou um circuito em 1918. Entretanto, John M. Miller patenteou os seus modelos de circuito e os de George Washington Pierce em 1931, e após uma disputa legal, Pierce patenteou novamente os dois circuitos em 1938.[4] Historicamente, os primeiros osciladores foram válvulas termiônicas, as quais possuíam um pequeno tempo de vida útil e alto custo de manutenção. Consequentemente, havia uma grande vantagem em se utilizar circuitos de uma válvula ao invés de circuitos de duas válvulas. Uma forte ênfase foi dada em se conseguir o máximo de força de saída do circuito oscilador, desde que isso significou menos válvulas de amplificação de força seriam necessários em uma transmissão. Válvulas termiônicas são operadas supridas com uma voltagem de 150-300 VDC, a qual permitem grande balanço de voltagem e são extremamente fáceis de extenuar o limite de dissipação do cristal ou uma quebra do cristal.
Com o advento do transistor e dos circuitos integrados, a ênfase foi colocada no desempenho. Transistores são bem pequenos e possui uma vida útil indefinida, então em muitos casos o número de transistores usados em um circuito oscilador é quase irrelevante. A pequena tensão de alimentação usadas em circuitos integrados reduziu o problema de esgotamento do cristal em quantidades significativas. E para obter melhor estabilidade de frequência, circuitos osciladores são frequentemente projetados com uma saída de baixa potência, uma vez que é mais simples de se usar um amplificador.
Circuitos Osciladores
editarPara produzir sinais de baixa frequência ou de alta frequência são utilizados os circuitos osciladores. De modo geral, um circuito oscilador é um amplificador que é montado de modo que sua saída possui frequência e amplitude definida. A maneira que cada oscilador funciona determina o seu tipo. Entre eles, existem o Oscilador Hartley, Oscilador Colpitts, Oscilador de Bloqueio, Oscilador de Duplo T, Oscilador de Deslocamento de Fase, Multivibrador Astável, Oscilador de Relaxação, Oscilador de modo paralelo e o Oscilador de Cristal.[5]
A velocidade de aplicação do sinal na entrada do circuito determina o tempo de percurso do mesmo até um ciclo completo, e, portanto, a frequência de operação o oscilador. Para isto, é importante que o ganho (gain) do sinal seja maior que 1. O que significa que o sinal de saída deve ter um valor maior do que o sinal de entrada. Se, ao contrário, o ganho do sinal for menor do que 1, o sinal de saída irá se enfraquecer em cada ciclo, causando a denominada “oscilação amortecida”. E por sua vez, o sinal de ganho igual a 1 não possui utilidade, porque para gerar a oscilação, é necessário que o valor adicional do sinal de saída seja utilizado para oscilar o circuito, o que não ocorre neste caso.
Oscilador de Cristal
editarOs materiais piezoelétricos são materiais que quando submetidos a compressão mecânica geram uma diferença de potencial bem específica, e inversamente, a aplicação de uma diferença de potencial provoca uma deformação mecânica. O cristal de piezoelétrico mais comum é o cristal de quartzo. Estes cristais são encontrados em estado bruto na forma de bastões com secção hexagonal, para a criação do cristal oscilador, o material bruto é cortado em lâminas finas. E a frequência de ressonância da lâmina será determinada pelas dimensões mecânicas do cristal no momento do seu corte.[2]
A frequência de ressonância de um cristal de quartzo está aproximadamente entre 1 KHz e 200 MHz, sendo o limite inferior da frequência específica para lâminas grandes de cristal e o limite superior de frequência específica para lâminas pequenas de cristal.
Tipos de osciladores de cristal
editarOs os osciladores de cristal são classificados em diversos tipos, dependendo da aplicação.[6][7]
- SPXO
- TCXO
- VCXO
- OCXO
Fundamentos da Oscilação de Quartzo
editarOscilação
editarUm circuito que oscila irá ter um feedback positivo e um ganho maior que 1. Com um cristal como uma série de elementos no loop e sem nenhum outro elemento sensível a frequência no circuito, ele irá oscilar na frequência de ressonância fundamental do cristal.
Quando o feedback do circuito oscilar é primeiramente fechado, um sinal de onda de oscilação senoidal começa, e a amplitude aumenta até que a sobrecarga (overload) ocorra. Osciladores de cristal podem usualmente fornecer tanto uma saída de onda quadrada (square wave output) quanto um sinal de onda senoidal (sine wave output). Sendo que o sinal guiando o cristal mais comum é o sinal de onda quadrado, e o sinal de saída de saída do cristal é sempre uma onda senoidal. Ambos os sinais de onda podem ser usados para uma saída, drenando o ponto de circuito apropriado.
Ressonância em série versus ressonância em paralelo
editarNão existe algo como uma ressonância paralela no oscilador de cristal. Todos os cristais osciladores operam na ressonância em série ou próxima dela. O significado usual de ressonância paralela é que o cristal possui um alto valor de impedância através dos terminais. Esse fato se destaca com a ressonância em série, a qual usualmente significa que o cristal possui um baixo valor de impedância através dos seus terminais. Ressonância em série existe fisicamente no cristal, mas a ressonância paralela existe somente como um fenômeno de medição do cristal. Quando uma impedância do cristal é medida externamente com uma função de frequência, um pico será encontrado acima da ressonância em série, onde parte da indutância L do movimento relativo ressoa paralelamente com o desvio terminal do cristal de capacitância C.[8]
Do ponto de vista do circuito, o desvio terminal de capacitância C do cristal deveria ser considerada como parte da carga externa do cristal, e não como parte elementos de sua frequência controlada L e C. Dados obtidos experimentalmente confirmam esse ponto de vista. Quando a ressonância paralela é mencionada, ela possui o significado de que o cristal possui alto valor de impedância através dos terminais, e não que o cristal esteja oscilando em uma frequência maior onde a entrada impedância do pico do cristal ocorre.[8]
Modelo Matemático
editarMatematicamente a impedância do circuito pode ser obtida por meio das equações:
ou
tal que s é a frequência complexa, é a frequência angular ressonante em serie, e é a frequência angular ressonante em paralelo.[9]
Modo de Funcionamento
editarOs cristais de quartzo, quando são excitados eletricamente tendem a vibrar em uma frequência, a qual depende do corte que foi feito no quartzo e também das suas dimensões. A influência do cristal de excitação funciona como placas de um capacitor. Nele, deve ser considerada além da resistência, também a indutância dos terminais. Entretanto, devido à tensão gerada pelo cristal quando vibra, e também a sua sensibilidade, é possível criar circuitos em que esse é utilizado como controle de frequência.[3]
Aplicações
editarOs osciladores são aplicados em diversos componentes eletrônicos tais como:[6]
- Relógios;
- Computadores;
- Telefones sem fio;
- Telefones celulares;
- Instrumentos de medida de diversos tipos;
- Televisores;
- DVDs.
Referências
- ↑ «Crystal oscillators» (em inglês). Consultado em 9 de março de 2021
- ↑ a b c Malvino, Albert; Bates, David (2016). Eletrônica. 2. Traduzido por Antonio Pertence Jr. Porto Alegre: AMGH Editora Ltda. p. 920. ISBN 9780073373881
- ↑ a b Floyd, Thomas L. (2018). Electronic Devices. Harlow: Pearson. p. 831. ISBN 978-1-29-222299-8
- ↑ «Generating and transmitting electric currents» (em inglês). Consultado em 9 de março de 2021
- ↑ Antonio Vargas Pinto, Luiz (2000). «Osciladores» (PDF). Consultado em 9 de março de 2021
- ↑ a b «Quartz crystal device». https://www.qiaj.jp/pages/top/index-e.html (em inglês). Consultado em 9 de março de 2021
- ↑ «Introduction to Quartz Frequency Standards - Oscillator Categories». https://ieee-uffc.org/ (em inglês). Consultado em 9 de março de 2021. Cópia arquivada em 19 de março de 2016
- ↑ a b Matthys, Robert J. (1992). Crystal Oscillator Circuits. Malabar, Florida: Krieger Publishing Company. p. 9
- ↑ «Design of Crystal Oscillator Circuits» (PDF) (em inglês). Consultado em 9 de março de 2021
Ver também
editar
