Os polinômios de Hermite são um exemplo de polinômios ortogonais cujo principal campo de aplicação encontra-se na mecânica quântica , especialmente no estudo do oscilador harmônico unidimensional. São nomeados assim em homenagem a Charles Hermite .
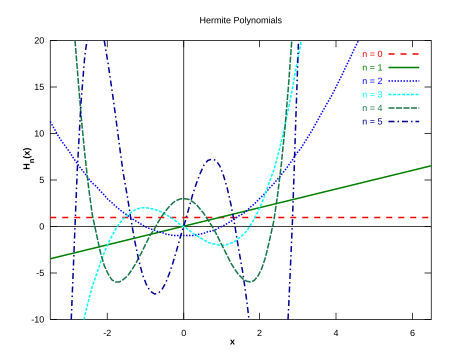
Os cinco primeiros polinômios de Hermite (probabilísticos).
Os polinômios de Hermite ("polinômios de Hermite probabilísticos") são definidos por:
H
n
(
x
)
=
(
−
1
)
n
e
x
2
/
2
d
n
d
x
n
e
−
x
2
/
2
{\displaystyle H_{n}(x)=(-1)^{n}e^{x^{2}/2}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}/2}\,\!}
Ou, às vezes, por ("polinômios de Hermite físicos")
H
n
p
h
y
s
(
x
)
=
(
−
1
)
n
e
x
2
d
n
d
x
n
e
−
x
2
{\displaystyle H_{n}^{\mathrm {phys} }(x)=(-1)^{n}e^{x^{2}}{\frac {d^{n}}{dx^{n}}}e^{-x^{2}}\,\!}
Essas definições não são exatamente equivalentes: uma é o redimensionamento da outra:
H
n
p
h
y
s
(
x
)
=
2
n
/
2
H
n
p
r
o
b
(
2
x
)
{\displaystyle H_{n}^{\mathrm {phys} }(x)=2^{n/2}H_{n}^{\mathrm {prob} }({\sqrt {2}}\,x)\,\!}
Os polinômios físicos podem ser escritos como:
H
n
p
h
y
s
(
x
)
=
(
2
x
)
n
−
n
(
n
−
1
)
1
!
(
2
x
)
n
−
2
+
n
(
n
−
1
)
(
n
−
2
)
(
n
−
3
)
2
!
(
2
x
)
n
−
4
−
…
{\displaystyle H_{n}^{\mathrm {phys} }(x)=(2x)^{n}-{\frac {n(n-1)}{1!}}(2x)^{n-2}+{\frac {n(n-1)(n-2)(n-3)}{2!}}(2x)^{n-4}-\dots }
H n x ) é um polinômio de grau n , com n = 0, 1, 2, 3 ... . Esses polinômios são ortogonais com relação à função peso
e
−
x
2
/
2
{\displaystyle e^{-x^{2}/2}\,\!}
ou
e
−
x
2
{\displaystyle e^{-x^{2}}\,\!}
ou seja,
∫
−
∞
∞
H
n
(
x
)
H
m
(
x
)
e
−
x
2
/
2
d
x
{\displaystyle \int _{-\infty }^{\infty }H_{n}(x)H_{m}(x)\,e^{-x^{2}/2}\,dx}
ou
∫
−
∞
∞
H
n
(
x
)
H
m
(
x
)
e
−
x
2
d
x
=
n
!
2
n
π
δ
n
m
{\displaystyle \int _{-\infty }^{\infty }H_{n}(x)H_{m}(x)\,e^{-x^{2}}\,dx={n!2^{n}}{\sqrt {\pi }}~\delta _{\mathit {nm}}}
onde
δ
n
m
{\displaystyle \delta _{\mathit {nm}}}
delta de Kronecker , que é igual à unidade quando
n
=
m
{\displaystyle n=m}
função densidade de probabilidade normal.
e
2
t
x
−
t
2
=
∑
n
=
0
∞
H
n
p
h
y
s
(
x
)
t
n
n
!
{\displaystyle e^{2tx-t^{2}}=\sum _{n=0}^{\infty }{\frac {H_{n}^{\mathrm {phys} }(x)t^{n}}{n!}}}
editar
Os polinômios de Hermite (na forma "física") satisfazem as seguintes relações de recorrência:
H
n
+
1
p
h
y
s
(
x
)
=
2
x
H
n
p
h
y
s
(
x
)
−
2
n
H
n
−
1
p
h
y
s
(
x
)
{\displaystyle H_{n+1}^{\mathrm {phys} }(x)=2xH_{n}^{\mathrm {phys} }(x)-2nH_{n-1}^{\mathrm {phys} }(x)}
H
′
n
p
h
y
s
(
x
)
=
2
n
H
n
−
1
p
h
y
s
(
x
)
{\displaystyle {H'}_{n}^{\mathrm {phys} }(x)=2nH_{n-1}^{\mathrm {phys} }(x)}
editar
Qualquer função f contínua pode ser expressa como uma série infinita em termos dos polinômios de Hermite:
f
(
x
)
=
∑
n
=
0
∞
A
n
H
n
(
x
)
=
A
0
H
0
(
x
)
+
A
1
H
1
(
x
)
+
A
2
H
2
(
x
)
+
…
{\displaystyle f(x)=\sum _{n=0}^{\infty }A_{n}H_{n}(x)=A_{0}H_{0}(x)+A_{1}H_{1}(x)+A_{2}H_{2}(x)+\ldots }
Onde as constantes são dadas por:
A
k
=
1
2
k
k
!
π
∫
−
∞
+
∞
e
−
x
2
f
(
x
)
H
k
(
x
)
d
x
{\displaystyle A_{k}={\frac {1}{2^{k}k!{\sqrt {\pi }}}}\int _{-\infty }^{+\infty }e^{-x^{2}}f(x)H_{k}(x)\ dx}
editar
Os polinômios de Hermite satisfazem:
H
n
(
−
x
)
=
(
−
1
)
n
H
n
(
x
)
{\displaystyle H_{n}(-x)=(-1)^{n}H_{n}(x)\,}
Logo
H
n
(
x
)
{\displaystyle H_{n}(x)}
função par para um
n
{\displaystyle n}
n
=
{
0
,
2
,
4
,
.
.
.
}
{\displaystyle n\ =\ \{0,2,4,...\}}
n
{\displaystyle n}
n
=
{
1
,
3
,
5
,
.
.
.
}
{\displaystyle n\ =\ \{1,3,5,...\}}
H
2
n
−
1
(
0
)
=
0
{\displaystyle H_{2n-1}(0)=0\,}
H
2
n
p
h
y
s
(
0
)
=
(
−
1
)
n
2
n
(
1
⋅
3
⋅
5
⋅
⋯
⋅
(
2
n
−
1
)
)
{\displaystyle H_{2n}^{\mathrm {phys} }(0)=(-1)^{n}2^{n}(1\cdot 3\cdot 5\cdot \dots \cdot (2n-1))}
editar
Os polinômios de Hermite são soluções da equação diferencial de Hermite:[ 1]
d
2
y
d
x
2
−
2
x
d
y
d
x
+
2
n
y
=
0
{\displaystyle {\frac {d^{2}y}{dx^{2}}}-2x{\frac {dy}{dx}}+2ny=0}
Que na forma canônica pode ser escrita como:
1
e
−
x
2
d
d
x
(
e
−
x
2
d
y
d
x
)
+
2
n
y
=
0
{\displaystyle {\frac {1}{e^{-x^{2}}}}{\frac {d}{dx}}\left(e^{-x^{2}}{\frac {dy}{dx}}\right)+2ny=0}
↑ Spiegel & Abellanas, 1992, p.158.
Spiegel, Murray R.; Abellanas, Lorenzo. McGraw-Hill, ed. Fórmulas y tablas de matemática aplicada . Aravaca (Madrid): [s.n.] ISBN 84-7615-197-7