Desvio para o vermelho
Na física, um desvio para o vermelho é um aumento no comprimento de onda e uma diminuição correspondente na frequência e na energia do fóton da radiação eletromagnética (como a luz).[1] A mudança oposta, uma diminuição no comprimento de onda e um aumento simultâneo na frequência e na energia, é conhecida como desvio para o vermelho negativo ou desvio para o azul. Os termos derivam das cores vermelho e azul que formam os extremos do espectro de luz visível.
Na astronomia e cosmologia, as três principais causas do desvio para o vermelho eletromagnético são
- A radiação viaja entre objetos que estão se afastando (desvio para o vermelho "relativístico", um exemplo do efeito Doppler relativístico).
- A radiação viaja em direção a um objeto em um potencial gravitacional mais fraco, ou seja, em direção a um objeto em um espaço-tempo menos fortemente curvo (mais plano) (desvio para o vermelho gravitacional).
- A radiação viaja através do espaço em expansão (desvio para o vermelho cosmológico). A observação de que todas as fontes de luz suficientemente distantes apresentam um desvio para o vermelho correspondente à sua distância da Terra é conhecida como lei de Hubble.
Desvios para o vermelho relativísticos, gravitacionais e cosmológicos podem ser entendidos sob o guarda-chuva das leis de transformação de quadros. As ondas gravitacionais, que também viajam à velocidade da luz, estão sujeitas aos mesmos fenômenos de desvio para o vermelho.
Exemplos de desvios para o vermelho fortes são um raio gama percebido como um raio-X, ou luz inicialmente visível percebida como ondas de rádio. Desvios para o vermelho mais sutis são vistos nas observações espectroscópicas de objetos astronômicos e são usados em tecnologias terrestres, como radar Doppler e armas de radar.
Existem outros processos físicos que podem levar a uma mudança na frequência da radiação eletromagnética, incluindo dispersão e efeitos ópticos; no entanto, as alterações resultantes são distinguíveis do desvio para o vermelho (astronômico) e geralmente não são referidas como tal (consulte a seção sobre óptica física e transferência radiativa).
O valor de um desvio para o vermelho é frequentemente denotado pela letra z, correspondente à mudança fracionária no comprimento de onda (positivo para desvios para o vermelho, negativo para desvios para o azul) e pela razão de comprimento de onda 1 + z (que é >1 para desvios para o vermelho, <1 para desvios para o azul).
História
editarA história do assunto começou com o desenvolvimento no século XIX da mecânica ondulatória e a exploração de fenômenos associados ao efeito Doppler. O efeito recebeu o nome de Christian Doppler, que ofereceu a primeira explicação física conhecida para o fenômeno em 1842.[2] A hipótese foi testada e confirmada para ondas sonoras pelo cientista holandês Christoph Buys-Ballot em 1845.[3] Doppler previu corretamente que o fenômeno deveria se aplicar a todas as ondas e, em particular, sugeriu que as cores variadas das estrelas poderiam ser atribuídas ao seu movimento em relação à Terra.[4] Antes que isso fosse verificado, no entanto, descobriu-se que as cores estelares eram principalmente devido à temperatura de uma estrela, não ao movimento. Só mais tarde o Doppler foi justificado por observações verificadas de desvio para o vermelho.
O primeiro desvio para o vermelho Doppler foi descrito pelo físico francês Hippolyte Fizeau em 1848, que apontou para o desvio nas linhas espectrais vistas nas estrelas como sendo devido ao efeito Doppler. O efeito às vezes é chamado de "efeito Doppler-Fizeau". Em 1868, o astrônomo britânico William Huggins foi o primeiro a determinar a velocidade de uma estrela se afastando da Terra por esse método.[5] Em 1871, o desvio para o vermelho óptico foi confirmado quando o fenômeno foi observado em linhas de Fraunhofer usando rotação solar, cerca de 0.1 Å no vermelho.[6] Em 1887, Vogel e Scheiner descobriram o efeito Doppler anual, a mudança anual no deslocamento Doppler das estrelas localizadas perto da eclíptica devido à velocidade orbital da Terra.[7] Em 1901, Aristarkh Belopolsky verificou o desvio para o vermelho óptico no laboratório usando um sistema de espelhos rotativos.[8]
A primeira ocorrência do termo red-shift impresso (nesta forma hifenizada) parece ser do astrônomo americano Walter Sydney Adams em 1908, no qual ele menciona "Dois métodos de investigação da natureza do desvio para o vermelho nebular".[9] A palavra não aparece sem hífen até cerca de 1934 por Willem de Sitter, talvez indicando que até então seu equivalente alemão, Rotverschiebung, era mais comumente usado.[10]
Começando com observações em 1912, Vesto M. Slipher descobriu que a maioria das galáxias espirais, então principalmente consideradas nebulosas espirais, tinham desvios para o vermelho consideráveis. Slipher relata pela primeira vez sua medição no volume inaugural do Lowell Observatory Bulletin.[11] Três anos depois, ele escreveu uma resenha na revista Popular Astronomy.[12] Nele, ele afirma que "a descoberta inicial de que a grande espiral de Andrômeda tinha a velocidade bastante excepcional de –300 km(/s) mostrou os meios então disponíveis, capazes de investigar não apenas os espectros das espirais, mas também suas velocidades".[13] Slipher relatou as velocidades de 15 nebulosas espirais espalhadas por toda a esfera celeste, todas menos três tendo velocidades "positivas" (ou seja, recessivas) observáveis. Posteriormente, Edwin Powell Hubble descobriu uma relação aproximada entre os desvios para o vermelho de tais "nebulosas" e as distâncias a eles com a formulação de sua lei de Hubble homônima.[14] Essas observações corroboraram o trabalho de 1922 de Alexander Friedmann, no qual ele derivou as equações de Friedmann–Lemaître.[15] Eles são hoje considerados fortes evidências de um universo em expansão e da teoria do Big Bang.[16]
Medição, caracterização e interpretação
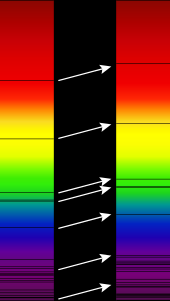
editarO espectro de luz que vem de uma fonte (veja a ilustração do espectro idealizado no canto superior direito) pode ser medido. Para determinar o desvio para o vermelho, busca-se características no espectro, como linhas de absorção, linhas de emissão ou outras variações na intensidade da luz. Se encontrados, esses recursos podem ser comparados com recursos conhecidos no espectro de vários compostos químicos encontrados em experimentos onde esse composto está localizado na Terra. Um elemento atômico muito comum no espaço é o hidrogênio. O espectro da luz originalmente inexpressiva que brilhou através do hidrogênio mostrará um espectro de assinatura específico para o hidrogênio que possui características em intervalos regulares. Se restrito às linhas de absorção, seria semelhante à ilustração (canto superior direito). Se o mesmo padrão de intervalos é visto em um espectro observado de uma fonte distante, mas ocorrendo em comprimentos de onda deslocados, ele também pode ser identificado como hidrogênio. Se a mesma linha espectral for identificada em ambos os espectros, mas em diferentes comprimentos de onda, o desvio para o vermelho pode ser calculado usando a tabela abaixo. Determinar o desvio para o vermelho de um objeto dessa maneira requer uma faixa de frequência ou comprimento de onda. Para calcular o desvio para o vermelho, é preciso conhecer o comprimento de onda da luz emitida no quadro de repouso da fonte: em outras palavras, o comprimento de onda que seria medido por um observador localizado adjacente e comovendo com a fonte. Como em aplicações astronômicas essa medição não pode ser feita diretamente, pois isso exigiria viajar até a estrela distante de interesse, o método usando linhas espectrais descrito aqui é usado. Desvios para o vermelho não podem ser calculados olhando para características não identificadas cuja frequência de quadro de repouso é desconhecida, ou com um espectro sem características ou ruído branco (flutuações aleatórias em um espectro).[18]
Desvio para o vermelho (e desvio para o azul) pode ser caracterizado pela diferença relativa entre os comprimentos de onda (ou frequência) observados e emitidos de um objeto. Em astronomia, costuma-se referir a essa mudança usando uma quantidade adimensional chamada z. Se λ representa o comprimento de onda e f representa a frequência (observe, λf = c onde c é a velocidade da luz), então z é definido pelas equações:[19]
| Com base no comprimento de onda | Com base na frequência |
|---|---|
Depois que z é medido, a distinção entre desvio para o vermelho e desvio para o azul é simplesmente uma questão de z ser positivo ou negativo. Por exemplo, os desvios para o azul do efeito Doppler (z < 0) estão associados a objetos que se aproximam do observador com a luz mudando para energias maiores. Por outro lado, os desvios para o vermelho do efeito Doppler (z > 0) estão associados a objetos que se afastam do observador com a luz mudando para energias mais baixas. Da mesma forma, os desvios para o azul gravitacionais estão associados à luz emitida por uma fonte que reside dentro de um campo gravitacional mais fraco, conforme observado de dentro de um campo gravitacional mais forte, enquanto o desvio para o vermelho gravitacional implica as condições opostas.
Fórmulas de desvios para o vermelho
editarNa relatividade geral, pode-se derivar várias fórmulas de casos especiais importantes para o desvio para o vermelho em certas geometrias de espaço-tempo especiais, conforme resumido na tabela a seguir. Em todos os casos, a magnitude do desvio (o valor de z) é independente do comprimento de onda.[20]
| Tipo de desvio para o vermelho |
Geometria | Fórmula[21] |
|---|---|---|
| Doppler relativístico | Espaço de Minkowski (espaço-tempo plano) |
Para movimento completamente na
|
| Desvio para o vermelho cosmológico | Espaço-tempo de FLRW (expandindo o universo do Big Bang) |
|
| Desvio para o vermelho gravitacional | qualquer espaço-tempo estacionário |
Para a geometria de Schwarzschild:
Em termos de velocidade de escape: para |
Efeito Doppler
editarSe uma fonte de luz está se afastando de um observador, ocorre o desvio para o vermelho (z > 0); se a fonte se move em direção ao observador, ocorre o desvio para o azul (z < 0). Isso é verdade para todas as ondas eletromagnéticas e é explicado pelo efeito Doppler. Consequentemente, esse tipo de desvio para o vermelho é chamado de desvio para o vermelho Doppler. Se a fonte se afasta do observador com velocidade v, que é muito menor que a velocidade da luz (v ≪ c), o desvio para o vermelho é dado por
- (desde )
onde c é a velocidade da luz. No efeito Doppler clássico, a frequência da fonte não é modificada, mas o movimento recessivo causa a ilusão de uma frequência mais baixa.
Um tratamento mais completo do desvio para o vermelho Doppler requer considerar os efeitos relativísticos associados ao movimento de fontes próximas à velocidade da luz. Uma derivação completa do efeito pode ser encontrada no artigo sobre o efeito Doppler relativístico. Em resumo, os objetos que se movem perto da velocidade da luz experimentarão desvios da fórmula acima devido à dilatação do tempo da relatividade especial que pode ser corrigida pela introdução do fator de Lorentz γ na fórmula Doppler clássica da seguinte forma (para movimento apenas na linha de visão):
Este fenômeno foi observado pela primeira vez em um experimento de 1938 realizado por Herbert E. Ives e G.R. Stilwell, chamado de experimento de Ives-Stilwell.[22]
Como o fator de Lorentz depende apenas da magnitude da velocidade, isso faz com que o desvio para o vermelho associado à correção relativística seja independente da orientação do movimento da fonte. Em contraste, a parte clássica da fórmula depende da projeção do movimento da fonte na linha de visão que produz resultados diferentes para diferentes orientações. Se θ é o ângulo entre a direção do movimento relativo e a direção de emissão no referencial do observador[23] (o ângulo zero está diretamente longe do observador), a forma completa para o efeito Doppler relativístico se torna:
e para movimento somente na linha de visão (θ = 0°), esta equação se reduz a:
Para o caso especial em que a luz está se movendo em ângulo reto (θ = 90°) para a direção do movimento relativo no quadro do observador,[24] o desvio para o vermelho relativístico é conhecido como desvio para o vermelho transversal e desvio para o vermelho:
é medido, mesmo que o objeto não esteja se afastando do observador. Mesmo quando a fonte está se movendo em direção ao observador, se houver um componente transversal ao movimento, então há alguma velocidade na qual a dilatação apenas cancela o desvio para o azul esperado e, em velocidades mais altas, a fonte que se aproxima será desviada para o vermelho.[25]
Expansão do espaço
editarNa primeira parte do século XX, Vesto M. Slipher, Wirtz e outros fizeram as primeiras medições dos desvios para o vermelho e para o azul das galáxias além da Via Láctea. Eles inicialmente interpretaram esses desvios para o vermelho e desvios para o azul como sendo devido a movimentos aleatórios, mas depois Lemaître (1927) e Hubble (1929), usando dados anteriores, descobriram uma correlação aproximadamente linear entre os desvios para o vermelho crescentes e as distâncias para as galáxias. Lemaître percebeu que essas observações poderiam ser explicadas por um mecanismo de produção de desvios para o vermelho visto nas soluções de Friedmann para as equações de Einstein da relatividade geral. A correlação entre desvios para o vermelho e distâncias é exigida por todos esses modelos que possuem uma expansão métrica do espaço.[16] Como resultado, o comprimento de onda dos fótons que se propagam pelo espaço em expansão é esticado, criando o desvio para o vermelho cosmológico.
Há uma distinção entre um desvio para o vermelho no contexto cosmológico em comparação com o observado quando objetos próximos exibem um desvio para o vermelho local do efeito Doppler. Em vez de desvios para o vermelho cosmológicos serem uma consequência das velocidades relativas que estão sujeitas às leis da relatividade especial (e, portanto, sujeitas à regra de que dois objetos separados localmente não podem ter velocidades relativas entre si mais rápidas que a velocidade da luz), os fótons, em vez disso, aumentam em comprimento de onda e desvio para o vermelho devido a uma característica global do espaço-tempo através do qual estão viajando. Uma interpretação desse efeito é a ideia de que o próprio espaço está se expandindo.[26] Devido à expansão aumentando à medida que as distâncias aumentam, a distância entre duas galáxias remotas pode aumentar em mais de 3×108 m/s, mas isso não implica que as galáxias se movam mais rápido que a velocidade da luz em sua localização atual (o que é proibido pela covariância de Lorentz).
Derivação matemática
editarAs consequências observacionais desse efeito podem ser derivadas usando as equações da relatividade geral que descrevem um universo homogêneo e isotrópico.
Para derivar o efeito de desvio para o vermelho, use a equação geodésica para uma onda de luz, que é
onde
- ds é o intervalo espaço-tempo
- dt é o intervalo de tempo
- dr é o intervalo espacial
- c é a velocidade da luz
- a é o fator de escala cósmica dependente do tempo
- k é a curvatura por unidade de área.
Para um observador observando a crista de uma onda de luz em uma posição r = 0 e tempo t = tagora, a crista da onda de luz foi emitida em um tempo t = tem seguida no passado e em uma posição distante r = R. Integrando sobre o caminho no espaço e no tempo que a onda de luz viaja produz:
Em geral, o comprimento de onda da luz não é o mesmo para as duas posições e tempos considerados devido às propriedades variáveis da métrica. Quando a onda foi emitida, ela tinha um comprimento de onda λem seguida. A próxima crista da onda de luz foi emitida de cada vez
O observador vê a próxima crista da onda de luz observada com um comprimento de onda λagora para chegar em um momento
Como a crista subsequente é novamente emitida de r = R e é observada em r = 0, a seguinte equação pode ser escrita:
O lado direito das duas equações integrais acima são idênticos, o que significa
Usando a seguinte manipulação:
achamos que:
Para variações muito pequenas no tempo (durante o período de um ciclo de uma onda de luz), o fator de escala é essencialmente uma constante ((a = an hoje e a = at antes). Isso rende
que pode ser reescrita como
Usando a definição de desvio para o vermelho fornecida acima, a equação
é obtido. Em um universo em expansão como o que habitamos, o fator de escala está aumentando monotonicamente com o passar do tempo, assim, z é positivo e galáxias distantes aparecem com desvio para o vermelho.
Usando um modelo de expansão do universo, o desvio para o vermelho pode ser relacionado à idade de um objeto observado, a chamada relação tempo cósmico-desvio para o vermelho. Denote uma razão de densidade como Ω0:
com ρcrit a densidade crítica demarcando um universo que eventualmente se rompe de um que simplesmente se expande. Essa densidade é de cerca de três átomos de hidrogênio por metro cúbico de espaço.[27] Em grandes desvios para o vermelho, 1 + z > Ω0−1, encontra-se:
onde H0 é a constante de Hubble atual e z é o desvio para o vermelho.[28][29][30]
Distinção entre efeitos cosmológicos e locais
editarPara desvios para o vermelho cosmológicos de z < 0.01, desvios para o vermelho Doppler adicionais e desvios para o azul devido aos movimentos peculiares das galáxias em relação umas às outras causam uma ampla dispersão da Lei de Hubble padrão.[31] A situação resultante pode ser ilustrada pela Expansão do Universo de Folhas de Borracha, uma analogia cosmológica comum usada para descrever a expansão do espaço. Se dois objetos são representados por rolamentos de esferas e o espaço-tempo por uma folha de borracha esticada, o efeito Doppler é causado rolando as bolas pela folha para criar um movimento peculiar. O desvio para o vermelho cosmológico ocorre quando os rolamentos de esferas estão presos à folha e a folha é esticada.[32][33][34]
Os desvios para o vermelho das galáxias incluem tanto um componente relacionado à velocidade de recessão da expansão do universo quanto um componente relacionado ao movimento peculiar (deslocamento Doppler).[35] O desvio para o vermelho devido à expansão do universo depende da velocidade de recessão de uma forma determinada pelo modelo cosmológico escolhido para descrever a expansão do universo, que é muito diferente de como o desvio para o vermelho Doppler depende da velocidade local.[36] Descrevendo a origem da expansão cosmológica do desvio para o vermelho, o cosmólogo Edward Robert Harrison disse: "A luz deixa uma galáxia, que está estacionária em sua região local do espaço, e é eventualmente recebida por observadores estacionários em sua própria região local do espaço. É tão simples quanto isso..."[37] Steven Weinberg esclareceu: "O aumento do comprimento de onda da emissão para a absorção da luz não depende da taxa de variação de a(t) [aqui a(t) é o Fator de escala Robertson-Walker] nos momentos de emissão ou absorção, mas no aumento de a(t) em todo o período de emissão a absorção".[38]
A literatura popular geralmente usa a expressão "desvio para o vermelho Doppler" em vez de "desvio para o vermelho cosmológico" para descrever o desvio para o vermelho de galáxias dominadas pela expansão do espaço-tempo, mas o desvio para o vermelho cosmológico não é encontrado usando a equação relativística de Doppler,[39] que é caracterizada por relatividade especial; assim v > c é impossível enquanto, em contraste, v > c é possível para desvios para o vermelho cosmológicos porque o espaço que separa os objetos (por exemplo, um quasar da Terra) pode se expandir mais rápido que a velocidade da luz.[40] Mais matematicamente, o ponto de vista de que "as galáxias distantes estão recuando" e o ponto de vista de que "o espaço entre as galáxias está se expandindo" estão relacionados por sistemas de coordenadas variáveis. Expressar isso com precisão requer trabalhar com a matemática da Métrica de Friedmann-Lemaître-Robertson-Walker.[41]
Se o universo estivesse se contraindo em vez de se expandir, veríamos galáxias distantes desviadas para o azul em uma quantidade proporcional à sua distância em vez de desviadas para o vermelho.[42]
Desvio para o vermelho gravitacional
editarNa teoria da relatividade geral, há dilatação do tempo dentro de um poço gravitacional. Isso é conhecido como desvio para o vermelho gravitacional ou desvio de Einstein.[43] A derivação teórica deste efeito decorre da solução de Schwarzschild das equações de Einstein, que produz a seguinte fórmula para o desvio para o vermelho associado a um fóton viajando no campo gravitacional de uma massa esfericamente simétrica não carregada, não rotativa:
onde
- G é a constante gravitacional,
- M é a massa do objeto que cria o campo gravitacional,
- r é a coordenada radial da fonte (que é análoga à distância clássica do centro do objeto, mas na verdade é uma coordenada de Schwarzschild), e
- c é a velocidade da luz.
Este resultado de desvio para o vermelho gravitacional pode ser derivado das suposições da relatividade especial e do princípio da equivalência; a teoria completa da relatividade geral não é necessária.[44]
O efeito é muito pequeno, mas mensurável na Terra usando o efeito Mössbauer e foi observado pela primeira vez no experimento de Pound-Rebka.[45] No entanto, é significativo perto de um buraco negro e, à medida que um objeto se aproxima do horizonte de eventos, o desvio para o vermelho se torna infinito. É também a causa dominante de grandes flutuações de temperatura em escala angular na radiação cósmica de fundo em micro-ondas (ver efeito Sachs-Wolfe).[46]
Observações na astronomia
editarO desvio para o vermelho observado na astronomia pode ser medido porque os espectros de emissão e absorção dos átomos são distintos e bem conhecidos, calibrados a partir de experimentos espectroscópicos em laboratórios na Terra. Quando o desvio para o vermelho de várias linhas de absorção e emissão de um único objeto astronômico é medido, z é notavelmente constante. Embora os objetos distantes possam ser levemente borrados e as linhas alargadas, isso não é mais do que pode ser explicado pelo movimento térmico ou mecânico da fonte. Por essas e outras razões, o consenso entre os astrônomos é que os desvios para o vermelho observados são devidos a alguma combinação das três formas estabelecidas de desvios para o vermelho do tipo Doppler. Hipóteses alternativas e explicações para desvio para o vermelho, como luz cansada, geralmente não são consideradas plausíveis.[47]
A espectroscopia, como medida, é consideravelmente mais difícil do que a simples fotometria, que mede o brilho de objetos astronômicos através de certos Filtros ópticos.[48] Quando os dados fotométricos são tudo o que está disponível (por exemplo, o Campo Profundo do Hubble e o Campo Ultra Profundo do Hubble), os astrônomos contam com uma técnica para medir desvios para o vermelho fotométricos.[49] Devido às amplas faixas de comprimento de onda em filtros fotométricos e as suposições necessárias sobre a natureza do espectro na fonte de luz, os erros para esses tipos de medições podem variar até δz = 0.5 e são muito menos confiáveis do que as determinações espectroscópicas.[50] No entanto, a fotometria permite pelo menos uma caracterização qualitativa de um desvio para o vermelho. Por exemplo, se um espectro semelhante ao do Sol tivesse um desvio para o vermelho de z = 1, seria mais brilhante no infravermelho do que na cor verde-amarelo associada ao pico de seu espectro de corpo negro, e a intensidade da luz será reduzida no filtrar por um fator de quatro, (1 + z)2. Tanto a taxa de contagem de fótons quanto a energia dos fótons são desviadas para o vermelho. (Veja a correção K para mais detalhes sobre as consequências fotométricas do desvio para o vermelho).[51]
Observações locais
editarEm objetos próximos (dentro de nossa galáxia Via Láctea), os desvios para o vermelho observados quase sempre estão relacionados às velocidades da linha de visão associadas aos objetos observados. Observações de tais desvios para o vermelho e desvios para o azul permitiram aos astrônomos medir velocidades e parametrizar as massas das estrelas em órbita em binários espectroscópicos, um método empregado pela primeira vez em 1868 pelo astrônomo britânico William Huggins.[5] Da mesma forma, pequenos desvios para o vermelho e desvios para o azul detectados nas medições espectroscópicas de estrelas individuais são uma maneira pela qual os astrônomos foram capazes de diagnosticar e medir a presença e as características de sistemas planetários em torno de outras estrelas e até fizeram medições diferenciais muito detalhadas de desvios para o vermelho durante trânsitos planetários para determinar parâmetros orbitais precisos.[52] Medições finamente detalhadas de desvios para o vermelho são usadas em heliosismologia para determinar os movimentos precisos da fotosfera do Sol.[53] Desvios para o vermelho também foram usados para fazer as primeiras medições das taxas de rotação de planetas,[54] velocidades de nuvens interestelares,[55] a rotação de galáxias,[20] e a dinâmica de acreção em estrelas de nêutrons e buracos negros que exibem ambos Doppler e desvios para o vermelho gravitacionais.[56] Além disso, as temperaturas de vários objetos emissores e absorventes podem ser obtidas medindo-se o alargamento Doppler, efetivamente desvios para o vermelho e desvios para o azul em uma única linha de emissão ou absorção.[57] Ao medir o alargamento e os deslocamentos da linha de hidrogênio de 21 centímetros em diferentes direções, os astrônomos foram capazes de medir as velocidades de recessão do gás interestelar, que por sua vez revela a curva de rotação da nossa Via Láctea.[20] Medidas semelhantes foram realizadas em outras galáxias, como Andrômeda.[20] Como ferramenta de diagnóstico, as medidas de desvio para o vermelho são uma das medidas espectroscópicas mais importantes feitas na astronomia.
Observações extragalácticas
editarOs objetos mais distantes exibem desvios para o vermelho maiores correspondentes ao fluxo de Hubble do universo. O maior desvio para o vermelho observado, correspondendo à maior distância e mais distante no tempo, é o da radiação cósmica de fundo em micro-ondas; o valor numérico de seu desvio para o vermelho é de cerca de z = 1089 (z = 0 corresponde ao tempo presente), e mostra o estado do universo cerca de 13.8 bilhões de anos atrás,[58] e 379.000 anos após os momentos iniciais do Big Bang.[59]
Os núcleos luminosos de quasares, semelhantes a pontos, foram os primeiros objetos de "alto desvio para o vermelho" (z > 0.1) descobertos antes que o aprimoramento dos telescópios permitisse a descoberta de outras galáxias de alto desvio para o vermelho.
Para galáxias mais distantes do que o Grupo Local e o Aglomerado de Virgem nas proximidades, mas dentro de 1.000 megaparsecs ou mais, o desvio para o vermelho é aproximadamente proporcional à distância da galáxia. Essa correlação foi observada pela primeira vez por Edwin Hubble e ficou conhecida como lei de Hubble. Vesto M. Slipher foi o primeiro a descobrir desvios para o vermelho galácticos, por volta do ano de 1912, enquanto Hubble correlacionava as medidas de Slipher com distâncias que ele media por outros meios para formular sua Lei. No modelo cosmológico amplamente aceito baseado na relatividade geral, o desvio para o vermelho é resultado principalmente da expansão do espaço: isso significa que quanto mais distante uma galáxia está de nós, mais o espaço se expandiu no tempo desde que a luz deixou aquela galáxia, assim, quanto mais a luz é esticada, mais desviada para o vermelho ela é, e mais rápido ela parece estar se afastando de nós. A lei de Hubble segue em parte o princípio copernicano.[60] Como geralmente não se sabe quão luminosos são os objetos, medir o desvio para o vermelho é mais fácil do que medições de distância mais diretas, de modo que o desvio para o vermelho às vezes é convertido na prática para uma medição de distância bruta usando a lei de Hubble.
As interações gravitacionais de galáxias entre si e aglomerados causam uma dispersão significativa no gráfico normal do diagrama de Hubble. As velocidades peculiares associadas às galáxias sobrepõem um traço grosseiro da massa de objetos virializados no universo. Esse efeito leva a fenômenos como galáxias próximas (como a Galáxia de Andrômeda) exibindo desvios para o azul à medida que caímos em direção a um baricentro comum, e mapas de aglomerados de desvio para o vermelho mostrando um efeito de dedos de deus devido à dispersão de velocidades peculiares em uma distribuição aproximadamente esférica.[60] Esse componente adicionado dá aos cosmólogos a chance de medir as massas dos objetos independentemente da proporção massa-luz (a razão entre a massa de uma galáxia em massas solares e seu brilho em luminosidades solares), uma ferramenta importante para medir a matéria escura.[61]
A relação linear da lei de Hubble entre distância e desvio para o vermelho assume que a taxa de expansão do universo é constante. No entanto, quando o universo era muito mais jovem, a taxa de expansão e, portanto, a "constante" de Hubble era maior do que é hoje. Para galáxias mais distantes, então, cuja luz tem viajado até nós por muito mais tempo, a aproximação da taxa de expansão constante falha, e a lei de Hubble torna-se uma relação integral não linear e dependente da história da taxa de expansão desde a emissão da luz da galáxia em questão. Observações da relação desvio para o vermelho-distância podem ser usadas, então, para determinar a história de expansão do universo e, portanto, o conteúdo de matéria e energia.
Embora se acredite que a taxa de expansão tenha diminuído continuamente desde o Big Bang, observações recentes da relação desvio para o vermelho-distância usando supernovas tipo Ia sugeriram que em tempos comparativamente recentes a taxa de expansão do universo começou a acelerar.
Maiores desvios para o vermelho
editarAtualmente, os objetos com os maiores desvios para o vermelho conhecidos são galáxias e os objetos que produzem erupções de raios gama. Os desvios para o vermelho mais confiáveis são de dados espectroscópicos, e o desvio para o vermelho espectroscópico mais confirmado de uma galáxia é o de GN-z11,[62] com um desvio para o vermelho de z = 11.1, correspondendo a 400 milhões de anos após o Big Bang. O recorde anterior era de UDFy-38135539[63] em um desvio para o vermelho de z = 8.6, correspondendo a 600 milhões de anos após o Big Bang. Um pouco menos confiáveis são os desvios para o vermelho de Lyman-break, o mais alto dos quais é a galáxia com lente A1689-zD1 em um desvio para o vermelho de z = 7.5[64][65] e o próximo mais alto sendo z = 7.0.[66] A erupção de raios gama observada mais distante com uma medida espectroscópica de desvio para o vermelho foi GRB 090423, que teve um desvio para o vermelho de z = 8.2.[67] O quasar mais distante conhecido, ULAS J1342+0928, está em z = 7.54.[68][69] A galáxia de rádio de desvio para o vermelho mais conhecida (TGSS1530) está a z = 5.72[70] e o material molecular de desvio para o vermelho mais conhecido é a detecção de emissão da molécula de CO do quasar SDSS J1148+5251 em z = 6.42.[71]
Extremely red objects (objetos extremamente vermelhos) (ERO), são fontes astronômicas de radiação que irradiam energia na parte vermelha e infravermelha próxima do espectro eletromagnético. Estas podem ser galáxias de explosão estelar que têm um alto desvio para o vermelho acompanhado de avermelhamento da poeira intermediária, ou podem ser galáxias elípticas altamente desviadas para o vermelho com uma população estelar mais velha (e, portanto, mais vermelha).[72] Objetos que são ainda mais vermelhos que ERO são chamados de Hyper extremely red objects (objetos hiper extremamente vermelhos) (HERO).[73]
A radiação cósmica de fundo em micro-ondas tem um desvio para o vermelho de z = 1089, correspondendo a uma idade de aproximadamente 379.000 anos após o Big Bang e uma distância adequada de mais de 46 bilhões de anos-luz.[74] A primeira luz ainda a ser observada das estrelas mais antigas da População III, não muito tempo depois que os átomos se formaram e o CMB deixou de ser absorvido quase completamente, pode ter desvios para o vermelho na faixa de 20 < z < 100.[75] Outros eventos de alto desvio para o vermelho previstos pela física, mas não observáveis atualmente, são o fundo de neutrinos cósmicos de cerca de dois segundos após o Big Bang (e um desvio para o vermelho superior a z > 1010)[76] e o fundo de onda gravitacional cósmica emitido diretamente da inflação em um desvio para o vermelho em excesso de z > 1025.[77]
Em junho de 2015, os astrônomos relataram evidências de estrelas da População III na galáxia Cosmos Redshift 7 em z = 6.60. Essas estrelas provavelmente existiram no universo primordial (ou seja, em alto desvio para o vermelho) e podem ter iniciado a produção de elementos químicos mais pesados que o hidrogênio, necessários para a formação posterior de planetas e vida como a conhecemos.[78][79]
Pesquisas de desvios para o vermelho
editarCom o advento dos telescópios automatizados e melhorias nos espectroscópios, várias colaborações foram feitas para mapear o universo no desvio para o vermelho. Ao combinar desvio para o vermelho com dados de posição angular, um levantamento de desvio para o vermelho mapeia a distribuição 3D da matéria dentro de um campo do céu. Essas observações são usadas para medir as propriedades da estrutura em grande escala do universo. A Grande Muralha, um vasto superaglomerado de galáxias com mais de 500 milhões de anos-luz de largura, fornece um exemplo dramático de uma estrutura em grande escala que as pesquisas de desvio para o vermelho podem detectar.[80]
A primeira pesquisa de desvio para o vermelho foi a CfA Redshift Survey, iniciada em 1977 com a coleta de dados inicial concluída em 1982.[81] Mais recentemente, o 2dF Galaxy Redshift Survey determinou a estrutura em grande escala de uma seção do universo, medindo os desvios para o vermelho em mais de 220.000 galáxias; a coleta de dados foi concluída em 2002, e o conjunto de dados final foi lançado em 30 de junho de 2003.[82] O Sloan Digital Sky Survey (SDSS), está em andamento desde 2013 e visa medir os desvios para o vermelho de cerca de 3 milhões de objetos.[83] O SDSS registrou desvios para o vermelho para galáxias de até 0.8 e esteve envolvido na detecção de quasares além de z = 6. O DEEP2 Redshift Survey usa os telescópios Keck com o novo espectrógrafo "DEIMOS"; uma continuação do programa piloto DEEP1, DEEP2 é projetado para medir galáxias fracas com desvios para o vermelho de 0,7 e acima, e, portanto, está planejado fornecer um complemento de alto desvio para o vermelho para SDSS e 2dF.[84]
Efeitos de ótica física ou transferência radiativa
editarAs interações e fenômenos resumidos nos assuntos de transferência radiativa e óptica física podem resultar em mudanças no comprimento de onda e na frequência da radiação eletromagnética. Nesses casos, os devios correspondem a uma transferência de energia física para a matéria ou outros fótons, e não por uma transformação entre referenciais. Tais mudanças podem ser de fenômenos físicos como efeitos de coerência ou dispersão de radiação eletromagnética, seja de partículas elementares carregadas, de partículas ou de flutuações do índice de refração em um meio dielétrico, como ocorre no fenômeno de rádio dos assobiadores de rádio.[20] Embora esses fenômenos sejam às vezes chamados de "desvios para o vermelho" e "desvios para o azul", em astrofísica as interações luz-matéria que resultam em mudanças de energia no campo de radiação são geralmente chamadas de "vermelhidão" em vez de "desvio para o vermelho", que, como um termo, é normalmente reservado para os efeitos discutidos acima.[20]
Em muitas circunstâncias, a dispersão faz com que a radiação fique vermelha porque a entropia resulta na predominância de muitos fótons de baixa energia sobre poucos de alta energia (enquanto conserva a energia total).[20] Exceto possivelmente sob condições cuidadosamente controladas, a dispersão não produz a mesma mudança relativa no comprimento de onda em todo o espectro; isto é, qualquer z calculado é geralmente uma função do comprimento de onda. Além disso, a dispersão de meios aleatórios geralmente ocorre em muitos ângulos, e z é uma função do ângulo de dispersão. Se ocorrer dispersão múltipla, ou as partículas espalhadas tiverem movimento relativo, geralmente também haverá distorção das linhas espectrais.[20]
Na astronomia interestelar, os espectros visíveis podem parecer mais vermelhos devido a processos de dispersão em um fenômeno conhecido como avermelhamento interestelar,[20] da mesma forma, a dispersão de Rayleigh causa o avermelhamento atmosférico do Sol visto no nascer ou pôr do sol e faz com que o resto do céu tenha uma cor azul. Este fenômeno é distinto do desvio para o vermelho porque as linhas espectroscópicas não são deslocadas para outros comprimentos de onda em objetos avermelhados e há um escurecimento e distorção adicionais associados ao fenômeno devido aos fótons sendo dispersados dentro e fora da linha de visão.
Desvio para o azul
editar- "Desvio para o azul" redireciona aqui. Para o termo usado em fotoquímica, veja Desvio hipsocrômico. Para o fenômeno político, veja Desvio para o azul (política). Para outros usos de "desvio para o azul", veja Desvio para o azul (desambiguação).
O oposto de um desvio para o vermelho é um desvio para o azul. Um desvio para o azul é qualquer diminuição no comprimento de onda (aumento na energia), com um aumento correspondente na frequência, de uma onda eletromagnética. Na luz visível, isso muda uma cor para a extremidade azul do espectro.
Desvio para o azul Doppler
editarO desvio para o azul Doppler é causado pelo movimento de uma fonte em direção ao observador. O termo se aplica a qualquer diminuição no comprimento de onda e aumento na frequência causada pelo movimento relativo, mesmo fora do espectro visível. Apenas objetos que se movem em velocidades quase relativísticas em direção ao observador são visivelmente mais azuis a olho nu, mas o comprimento de onda de qualquer fóton ou outra partícula refletida ou emitida é encurtado na direção da viagem.[85]
Desvio para o azul Doppler é usado na astronomia para determinar o movimento relativo:
- A Galáxia de Andrômeda está se movendo em direção à nossa Via Láctea dentro do Grupo Local; assim, quando observada da Terra, sua luz está passando por um desvio para o azul.
- Componentes de um sistema estelar binário serão desviados para o azul ao se moverem em direção à Terra
- Ao observar galáxias espirais, o lado girando em nossa direção terá um leve desvio para o azul em relação ao lado girando para longe de nós (veja a relação Tully-Fisher).
- Os blazares são conhecidos por impulsionar jatos relativísticos em nossa direção, emitindo radiação síncrotron e bremsstrahlung que parece desviado para o azul.
- Estrelas próximas, como a Estrela de Barnard, estão se movendo em nossa direção, resultando em um desvio para o azul muito pequeno.
- O desvio para o azul Doppler de objetos distantes com um z alto pode ser subtraído do desvio para o vermelho cosmológico muito maior para determinar o movimento relativo no universo em expansão.[86]
Desvio para o azul gravitacional
editarAo contrário do desvio para o azul Doppler relativo, causado pelo movimento de uma fonte em direção ao observador e, portanto, dependente do ângulo recebido do fóton, o desvio para o azul gravitacional é absoluto e não depende do ângulo recebido do fóton:
- Os fótons que saem de um objeto gravitante tornam-se menos energéticos. Essa perda de energia é conhecida como "desvio para o vermelho", pois os fótons no espectro visível parecem mais vermelhos. Da mesma forma, os fótons que caem em um campo gravitacional tornam-se mais energéticos e exibem um desvio para o azul. ... Observe que a magnitude do efeito de desvio para o vermelho (desvio para o azul) não é uma função do ângulo emitido ou do ângulo recebido do fóton, depende apenas de quão radialmente o fóton teve que subir (cair) no potencial poço.[87][88]
É uma consequência natural da conservação de energia e equivalência massa-energia, e foi confirmada experimentalmente em 1959 com o experimento de Pound-Rebka. O desvio para o azul gravitacional contribui para a radiação cósmica de fundo em micro-ondas (CMB) através do efeito Sachs-Wolfe: quando um poço gravitacional evolui enquanto um fóton está passando, a quantidade de desvio para o azul na aproximação será diferente da quantidade de desvio para o vermelho gravitacional à medida que sai da região.[89]
Atípicos azuis
editarExistem galáxias ativas distantes que mostram um desvio para o azul em suas linhas de emissão [O III]. Um dos maiores desvios para o azul é encontrado no quasar de linha estreita, PG 1543+489, que tem uma velocidade relativa de -1150 km/s.[86] Esses tipos de galáxias são chamados de "atípicos azuis".[86]
Desvio para o azul cosmológico
editarEm um universo hipotético passando por uma contração descontrolada do Big Crunch, um desvio para o azul cosmológico seria observado, com galáxias mais distantes sendo cada vez mais desviados para o azul, exatamente o oposto do desvio para o vermelho cosmológico realmente observado no presente universo em expansão.
Ver também
editarReferências
- ↑ Hawking, S. (2016). O universo numa casca de noz. [S.l.]: Editora Intrinseca. p. 292. ISBN 978-85-8057-889-8. Consultado em 9 de novembro de 2022
- ↑ Doppler, Christian (1846). Beiträge zur fixsternenkunde. 69. [S.l.]: Prague: G. Haase Söhne. Bibcode:1846befi.book.....D
- ↑ Maulik, Dev (2005). «Doppler Sonography: A Brief History». In: Maulik, Dev; Zalud, Ivica. Doppler Ultrasound in Obstetrics And Gynecology. [S.l.]: Springer. ISBN 978-3-540-23088-5
- ↑ O'Connor, John J.; Robertson, Edmund F. (1998). «Christian Andreas Doppler». MacTutor History of Mathematics archive. University of St Andrews
- ↑ a b Huggins, William (1868). «Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II». Philosophical Transactions of the Royal Society of London. 158: 529–564. Bibcode:1868RSPT..158..529H. doi:10.1098/rstl.1868.0022
- ↑ Reber, G. (1995). «Intergalactic Plasma». Astrophysics and Space Science. 227 (1–2): 93–96. Bibcode:1995Ap&SS.227...93R. doi:10.1007/BF00678069
- ↑ Pannekoek, A (1961). A History of Astronomy. [S.l.]: Dover. p. 451. ISBN 978-0-486-65994-7
- ↑ Bélopolsky, A. (1901). «On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle». Astrophysical Journal. 13: 15. Bibcode:1901ApJ....13...15B. doi:10.1086/140786
- ↑ Adams, Walter S. (1908). «Preliminary catalogue of lines affected in sun-spots». Contributions from the Solar Observatory of the Carnegie Institution of Washington: Carnegie Institution of Washington. Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington. 22: 1–21. Bibcode:1908CMWCI..22....1A Reprinted in Adams, Walter S. (1908). «Preliminary Catalogue of Lines Affected in Sun-Spots Region λ 4000 TO λ 4500». Astrophysical Journal. 27: 45. Bibcode:1908ApJ....27...45A. doi:10.1086/141524
- ↑ de Sitter, W. (1934). «On distance, magnitude, and related quantities in an expanding universe». Bulletin of the Astronomical Institutes of the Netherlands. 7: 205. Bibcode:1934BAN.....7..205D.
It thus becomes urgent to investigate the effect of the redshift and of the metric of the universe on the apparent magnitude and observed numbers of nebulae of given magnitude
- ↑ Slipher, Vesto (1912). «The radial velocity of the Andromeda Nebula». Lowell Observatory Bulletin. 1: 2.56–2.57. Bibcode:1913LowOB...2...56S.
The magnitude of this velocity, which is the greatest hitherto observed, raises the question whether the velocity-like displacement might not be due to some other cause, but I believe we have at present no other interpretation for it
- ↑ Slipher, Vesto (1915). «Spectrographic Observations of Nebulae». Popular Astronomy. 23: 21–24. Bibcode:1915PA.....23...21S
- ↑ Slipher, Vesto (1915). «Spectrographic Observations of Nebulae». Popular Astronomy. 23: 22. Bibcode:1915PA.....23...21S
- ↑ Hubble, Edwin (1929). «A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae». Proceedings of the National Academy of Sciences of the United States of America. 15 (3): 168–173. Bibcode:1929PNAS...15..168H. PMC 522427 . PMID 16577160. doi:10.1073/pnas.15.3.168
- ↑ Friedman, A. A. (1922). «Über die Krümmung des Raumes». Zeitschrift für Physik. 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580 English translation in Friedman, A. (1999). «On the Curvature of Space». General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741)
- ↑ a b This was recognized early on by physicists and astronomers working in cosmology in the 1930s. The earliest layman publication describing the details of this correspondence is Eddington, Arthur (1933). The Expanding Universe: Astronomy's 'Great Debate', 1900–1931. [S.l.]: Cambridge University Press (Reprint: ISBN 978-0-521-34976-5)
- ↑ «Hubble census finds galaxies at redshifts 9 to 12». ESA/Hubble Press Release. Consultado em 13 de dezembro de 2012
- ↑ See, for example, this 25 May 2004 press release from NASA's Swift space telescope that is researching gamma-ray bursts: "Measurements of the gamma-ray spectra obtained during the main outburst of the GRB have found little value as redshift indicators, due to the lack of well-defined features. However, optical observations of GRB afterglows have produced spectra with identifiable lines, leading to precise redshift measurements."
- ↑ See [1] for a tutorial on how to define and interpret large redshift measurements.
- ↑ a b c d e f g h i See Binney and Merrifeld (1998), Carroll and Ostlie (1996), Kutner (2003) for applications in astronomy.
- ↑ Where z = redshift; v|| = velocity parallel to line-of-sight (positive if moving away from receiver); c = speed of light; γ = Lorentz factor; a = scale factor; G = gravitational constant; M = object mass; r = radial Schwarzschild coordinate, gtt = t,t component of the metric tensor
- ↑ Ives, H.; Stilwell, G. (1938). «An Experimental study of the rate of a moving atomic clock». J. Opt. Soc. Am. 28 (7): 215–226. Bibcode:1938JOSA...28..215I. doi:10.1364/josa.28.000215
- ↑ Freund, Jurgen (2008). Special Relativity for Beginners. [S.l.]: World Scientific. p. 120. ISBN 978-981-277-160-5
- ↑ Ditchburn, R (1961). Light. [S.l.]: Dover. p. 329. ISBN 978-0-12-218101-6
- ↑ See "Photons, Relativity, Doppler shift Arquivado em 2006-08-27 no Wayback Machine " at the University of Queensland
- ↑ The distinction is made clear in Harrison, Edward Robert (2000). Cosmology: The Science of the Universe 2nd ed. [S.l.]: Cambridge University Press. p. 306ff. ISBN 978-0-521-66148-5
- ↑ Steven Weinberg (1993). The First Three Minutes: A Modern View of the Origin of the Universe 2nd ed. [S.l.]: Basic Books. p. 34. ISBN 9780-465-02437-7
- ↑ Lars Bergström; Ariel Goobar (2006). Cosmology and Particle Astrophysics 2nd ed. [S.l.]: Springer. p. 77, Eq.4.79. ISBN 978-3-540-32924-4
- ↑ M.S. Longair (1998). Galaxy Formation. [S.l.]: Springer. p. 161. ISBN 978-3-540-63785-1
- ↑ Yu N Parijskij (2001). «The High Redshift Radio Universe». In: Norma Sanchez. Current Topics in Astrofundamental Physics. [S.l.]: Springer. p. 223. ISBN 978-0-7923-6856-4
- ↑ Measurements of the peculiar velocities out to 5 Mpc using the Hubble Space Telescope were reported in 2003 by Karachentsev; et al. (2003). «Local galaxy flows within 5 Mpc». Astronomy and Astrophysics. 398 (2): 479–491. Bibcode:2003A&A...398..479K. arXiv:astro-ph/0211011 . doi:10.1051/0004-6361:20021566
- ↑ Theo Koupelis; Karl F. Kuhn (2007). In Quest of the Universe 5th ed. [S.l.]: Jones & Bartlett Publishers. p. 557. ISBN 978-0-7637-4387-1
- ↑ "It is perfectly valid to interpret the equations of relativity in terms of an expanding space. The mistake is to push analogies too far and imbue space with physical properties that are not consistent with the equations of relativity." Geraint F. Lewis; Francis, Matthew J.; Barnes, Luke A.; Kwan, Juliana; et al. (2008). «Cosmological Radar Ranging in an Expanding Universe». Monthly Notices of the Royal Astronomical Society. 388 (3): 960–964. Bibcode:2008MNRAS.388..960L. arXiv:0805.2197 . doi:10.1111/j.1365-2966.2008.13477.x
- ↑ Michal Chodorowski (2007). «Is space really expanding? A counterexample». Concepts Phys. 4 (1): 17–34. Bibcode:2007ONCP....4...15C. arXiv:astro-ph/0601171 . doi:10.2478/v10005-007-0002-2
- ↑ Bedran,M.L. (2002)"A comparison between the Doppler and cosmological redshifts" Am.J.Phys. 70, 406–408
- ↑ Edward Harrison (1992). «The redshift-distance and velocity-distance laws». Astrophysical Journal, Part 1. 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179. A pdf file can be found here [2].
- ↑ Harrison 2000, p. 315.
- ↑ Steven Weinberg (2008). Cosmology. [S.l.]: Oxford University Press. p. 11. ISBN 978-0-19-852682-7
- ↑ Odenwald & Fienberg 1993
- ↑ Speed faster than light is allowed because the expansion of the spacetime metric is described by general relativity in terms of sequences of only locally valid inertial frames as opposed to a global Minkowski metric. Expansion faster than light is an integrated effect over many local inertial frames and is allowed because no single inertial frame is involved. The speed-of-light limitation applies only locally. See Michal Chodorowski (2007). «Is space really expanding? A counterexample». Concepts Phys. 4 (1): 17–34. Bibcode:2007ONCP....4...15C. arXiv:astro-ph/0601171 . doi:10.2478/v10005-007-0002-2
- ↑ M. Weiss, What Causes the Hubble Redshift?, entry in the Physics FAQ (1994), available via John Baez's website
- ↑ This is only true in a universe where there are no peculiar velocities. Otherwise, redshifts combine as
- ↑ Chant, C. A. (1930). «Notes and Queries (Telescopes and Observatory Equipment – The Einstein Shift of Solar Lines)». Journal of the Royal Astronomical Society of Canada. 24: 390. Bibcode:1930JRASC..24..390C
- ↑ Einstein, A (1907). «Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen». Jahrbuch der Radioaktivität und Elektronik. 4: 411–462 See p. 458 The influence of a gravitational field on clocks
- ↑ Pound, R.; Rebka, G. (1960). «Apparent Weight of Photons». Physical Review Letters. 4 (7): 337–341. Bibcode:1960PhRvL...4..337P. doi:10.1103/PhysRevLett.4.337 . This paper was the first measurement.
- ↑ Sachs, R. K.; Wolfe, A. M. (1967). «Perturbations of a cosmological model and angular variations of the cosmic microwave background». Astrophysical Journal. 147 (73): 73. Bibcode:1967ApJ...147...73S. doi:10.1086/148982
- ↑ When cosmological redshifts were first discovered, Fritz Zwicky proposed an effect known as tired light. While usually considered for historical interests, it is sometimes, along with intrinsic redshift suggestions, utilized by nonstandard cosmologies. In 1981, H. J. Reboul summarised many alternative redshift mechanisms that had been discussed in the literature since the 1930s. In 2001, Geoffrey Burbidge remarked in a review that the wider astronomical community has marginalized such discussions since the 1960s. Burbidge and Halton Arp, while investigating the mystery of the nature of quasars, tried to develop alternative redshift mechanisms, and very few of their fellow scientists acknowledged let alone accepted their work. Moreover, Goldhaber; et al. (2001). «Timescale Stretch Parameterization of Type Ia Supernova B-Band Lightcurves». Astrophysical Journal. 558 (1): 359–386. Bibcode:2001ApJ...558..359G. arXiv:astro-ph/0104382 . doi:10.1086/322460 pointed out that alternative theories are unable to account for timescale stretch observed in type Ia supernovae
- ↑ For a review of the subject of photometry, consider Budding, E., Introduction to Astronomical Photometry, Cambridge University Press (September 24, 1993), ISBN 0-521-41867-4
- ↑ The technique was first described by Baum, W. A.: 1962, in G. C. McVittie (ed.), Problems of extra-galactic research, p. 390, IAU Symposium No. 15
- ↑ Bolzonella, M.; Miralles, J.-M.; Pelló, R., Photometric redshifts based on standard SED fitting procedures, Astronomy and Astrophysics, 363, p.476–492 (2000).
- ↑ A pedagogical overview of the K-correction by David Hogg and other members of the SDSS collaboration can be found at astro-ph.
- ↑ The Exoplanet Tracker is the newest observing project to use this technique, able to track the redshift variations in multiple objects at once, as reported in Ge, Jian; Van Eyken, Julian; Mahadevan, Suvrath; Dewitt, Curtis; et al. (2006). «The First Extrasolar Planet Discovered with a New‐Generation High‐Throughput Doppler Instrument». The Astrophysical Journal. 648 (1): 683–695. Bibcode:2006ApJ...648..683G. arXiv:astro-ph/0605247 . doi:10.1086/505699
- ↑ Libbrecht, Keng (1988). «Solar and stellar seismology» (PDF). Space Science Reviews. 47 (3–4): 275–301. Bibcode:1988SSRv...47..275L. doi:10.1007/BF00243557
- ↑ In 1871 Hermann Carl Vogel measured the rotation rate of Venus. Vesto Slipher was working on such measurements when he turned his attention to spiral nebulae.
- ↑ An early review by Oort, J. H. on the subject: Oort, J. H. (1970). «The formation of galaxies and the origin of the high-velocity hydrogen». Astronomy and Astrophysics. 7: 381. Bibcode:1970A&A.....7..381O
- ↑ Asaoka, Ikuko (1989). «X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole». Publications of the Astronomical Society of Japan. 41 (4): 763–778. Bibcode:1989PASJ...41..763A
- ↑ Rybicki, G. B. and A. R. Lightman, Radiative Processes in Astrophysics, John Wiley & Sons, 1979, p. 288 ISBN 0-471-82759-2
- ↑ «Cosmic Detectives». The European Space Agency (ESA). 2 de abril de 2013. Consultado em 25 de abril de 2013
- ↑ An accurate measurement of the cosmic microwave background was achieved by the COBE experiment. The final published temperature of 2.73 K was reported in this paper: Fixsen, D. J.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E., Jr.; Isaacman, R. B.; Mather, J. C.; Meyer, S. S.; Noerdlinger, P. D.; Shafer, R. A.; Weiss, R.; Wright, E. L.; Bennett, C. L.; Boggess, N. W.; Kelsall, T.; Moseley, S. H.; Silverberg, R. F.; Smoot, G. F.; Wilkinson, D. T.. (1994). "Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument", Astrophysical Journal, 420, 445. The most accurate measurement as of 2006 was achieved by the WMAP experiment.
- ↑ a b Peebles (1993).
- ↑ Binney, James; Scott Treimane (1994). Galactic dynamics. [S.l.]: Princeton University Press. ISBN 978-0-691-08445-9
- ↑ Oesch, P. A.; Brammer, G.; van Dokkum, P.; et al. (1 de março de 2016). «A Remarkably Luminous Galaxy at z=11.1 Measured with Hubble Space Telescope Grism Spectroscopy». The Astrophysical Journal. 819 (2): 129. Bibcode:2016ApJ...819..129O. arXiv:1603.00461 . doi:10.3847/0004-637X/819/2/129
- ↑ M.D. Lehnert; Nesvadba, NP; Cuby, JG; Swinbank, AM; et al. (2010). «Spectroscopic Confirmation of a galaxy at redshift z = 8.6». Nature. 467 (7318): 940–942. Bibcode:2010Natur.467..940L. PMID 20962840. arXiv:1010.4312 . doi:10.1038/nature09462
- ↑ Watson, Darach; Christensen, Lise; Knudsen, Kirsten Kraiberg; Richard, Johan; Gallazzi, Anna; Michałowski, Michał Jerzy (2015). «A dusty, normal galaxy in the epoch of reionization». Nature. 519 (7543): 327–330. Bibcode:2015Natur.519..327W. PMID 25731171. arXiv:1503.00002 . doi:10.1038/nature14164
- ↑ Bradley, L.; et al. (2008). «Discovery of a Very Bright Strongly Lensed Galaxy Candidate at z ~ 7.6». The Astrophysical Journal. 678 (2): 647–654. Bibcode:2008ApJ...678..647B. arXiv:0802.2506 . doi:10.1086/533519
- ↑ Egami, E.; et al. (2005). «Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218». The Astrophysical Journal. 618 (1): L5–L8. Bibcode:2005ApJ...618L...5E. arXiv:astro-ph/0411117 . doi:10.1086/427550
- ↑ Salvaterra, R.; Valle, M. Della; Campana, S.; Chincarini, G.; et al. (2009). «GRB 090423 reveals an exploding star at the epoch of re-ionization». Nature. 461 (7268): 1258–60. Bibcode:2009Natur.461.1258S. PMID 19865166. arXiv:0906.1578 . doi:10.1038/nature08445
- ↑ «Scientists observe supermassive black hole in infant universe». phys.org
- ↑ Bañados, Eduardo; Venemans, Bram P.; Mazzucchelli, Chiara; Farina, Emanuele P.; Walter, Fabian; Wang, Feige; Decarli, Roberto; Stern, Daniel; Fan, Xiaohui; Davies, Frederick B.; Hennawi, Joseph F.; Simcoe, Robert A.; Turner, Monica L.; Rix, Hans-Walter; Yang, Jinyi; Kelson, Daniel D.; Rudie, Gwen C.; Winters, Jan Martin (janeiro de 2018). «An 800-million-solar-mass black hole in a significantly neutral Universe at a redshift of 7.5». Nature. 553 (7689): 473–476. Bibcode:2018Natur.553..473B. PMID 29211709. arXiv:1712.01860 . doi:10.1038/nature25180
- ↑ Saxena, A. (2018). «Discovery of a radio galaxy at z = 5.72». Monthly Notices of the Royal Astronomical Society. 480 (2): 2733–2742. Bibcode:2018MNRAS.480.2733S. arXiv:1806.01191 . doi:10.1093/mnras/sty1996
- ↑ Walter, Fabian; Bertoldi, Frank; Carilli, Chris; Cox, Pierre; et al. (2003). «Molecular gas in the host galaxy of a quasar at redshift z = 6.42». Nature. 424 (6947): 406–8. Bibcode:2003Natur.424..406W. PMID 12879063. arXiv:astro-ph/0307410 . doi:10.1038/nature01821
- ↑ Smail, Ian; Owen, F. N.; Morrison, G. E.; Keel, W. C.; et al. (2002). «The Diversity of Extremely Red Objects». The Astrophysical Journal. 581 (2): 844–864. Bibcode:2002ApJ...581..844S. arXiv:astro-ph/0208434 . doi:10.1086/344440
- ↑ Totani, Tomonori; Yoshii, Yuzuru; Iwamuro, Fumihide; Maihara, Toshinori; et al. (2001). «Hyper Extremely Red Objects in the Subaru Deep Field: Evidence for Primordial Elliptical Galaxies in the Dusty Starburst Phase». The Astrophysical Journal. 558 (2): L87–L91. Bibcode:2001ApJ...558L..87T. arXiv:astro-ph/0108145 . doi:10.1086/323619
- ↑ Lineweaver, Charles; Tamara M. Davis (2005). «Misconceptions about the Big Bang». Scientific American. 292 (3): 36–45. Bibcode:2005SciAm.292c..36L. doi:10.1038/scientificamerican0305-36
- ↑ Naoz, S.; Noter, S.; Barkana, R. (2006). «The first stars in the Universe». Monthly Notices of the Royal Astronomical Society: Letters. 373 (1): L98–L102. Bibcode:2006MNRAS.373L..98N. arXiv:astro-ph/0604050 . doi:10.1111/j.1745-3933.2006.00251.x
- ↑ Lesgourgues, J; Pastor, S (2006). «Massive neutrinos and cosmology». Physics Reports. 429 (6): 307–379. Bibcode:2006PhR...429..307L. arXiv:astro-ph/0603494 . doi:10.1016/j.physrep.2006.04.001
- ↑ Grishchuk, Leonid P (2005). «Relic gravitational waves and cosmology». Physics-Uspekhi. 48 (12): 1235–1247. Bibcode:2005PhyU...48.1235G. arXiv:gr-qc/0504018 . doi:10.1070/PU2005v048n12ABEH005795
- ↑ Sobral, David; Matthee, Jorryt; Darvish, Behnam; Schaerer, Daniel; Mobasher, Bahram; Röttgering, Huub J. A.; Santos, Sérgio; Hemmati, Shoubaneh (4 de junho de 2015). «Evidence For POPIII-Like Stellar Populations In The Most Luminous LYMAN-α Emitters At The Epoch Of Re-Ionisation: Spectroscopic Confirmation». The Astrophysical Journal. 808 (2). 139 páginas. Bibcode:2015ApJ...808..139S. arXiv:1504.01734 . doi:10.1088/0004-637x/808/2/139
- ↑ Overbye, Dennis (17 de junho de 2015). «Astronomers Report Finding Earliest Stars That Enriched Cosmos». The New York Times. Consultado em 17 de junho de 2015
- ↑ M. J. Geller & J. P. Huchra, Science 246, 897 (1989). online
- ↑ See the official CfA website for more details.
- ↑ Shaun Cole; Percival; Peacock; Norberg; et al. (2005). «The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications». Mon. Not. R. Astron. Soc. 362 (2): 505–34. Bibcode:2005MNRAS.362..505C. arXiv:astro-ph/0501174 . doi:10.1111/j.1365-2966.2005.09318.x 2dF Galaxy Redshift Survey homepage Arquivado em 2007-02-05 no Wayback Machine
- ↑ «SDSS-III». www.sdss3.org
- ↑ Marc Davis; DEEP2 collaboration (2002). «Science objectives and early results of the DEEP2 redshift survey». Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002. Bibcode:2003SPIE.4834..161D. arXiv:astro-ph/0209419 . doi:10.1117/12.457897
- ↑ Kuhn, Karl F.; Theo Koupelis (2004). In Quest of the Universe. [S.l.]: Jones & Bartlett Publishers. pp. 122–3. ISBN 978-0-7637-0810-8
- ↑ a b c Aoki, Kentaro; Toshihiro Kawaguchi; Kouji Ohta (janeiro de 2005). «The Largest Blueshifts of the [O III] Emission Line in Two Narrow-Line Quasars». Astrophysical Journal. 618 (2): 601–608. Bibcode:2005ApJ...618..601A. arXiv:astro-ph/0409546 . doi:10.1086/426075
- ↑ R.J. Nemiroff (1993). «Gravitational Principles and Mathematics». NASA
- ↑ R. J. Nemiroff (1993). «Visual distortions near a neutron star and black hole». American Journal of Physics. 61 (7): 619–632. Bibcode:1993AmJPh..61..619N. arXiv:astro-ph/9312003v1 . doi:10.1119/1.17224
- ↑ Bonometto, Silvio; Gorini, Vittorio; Moschella, Ugo (2002). Modern Cosmology. [S.l.]: CRC Press. ISBN 978-0-7503-0810-6
Fontes
editarArtigos
editar- Odenwald, S. & Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" in Sky & Telescope Feb. 2003; pp31–35 (Este artigo é uma leitura útil para distinguir entre os 3 tipos de desvios para o vermelho e suas causas).
- Lineweaver, Charles H. and Tamara M. Davis, "Misconceptions about the Big Bang", Scientific American, March 2005. (Este artigo é útil para explicar o mecanismo cosmológico do desvio para o vermelho, bem como esclarecer equívocos sobre a física da expansão do espaço).
Livros
editar- Nussbaumer, Harry; Lydia Bieri (2009). Discovering the Expanding Universe. [S.l.]: Cambridge University Press. ISBN 978-0-521-51484-2
- Binney, James; Michael Merrifeld (1998). Galactic Astronomy. [S.l.]: Princeton University Press. ISBN 978-0-691-02565-0
- Carroll, Bradley W.; Dale A. Ostlie (1996). An Introduction to Modern Astrophysics. [S.l.]: Addison-Wesley Publishing Company, Inc. ISBN 978-0-201-54730-6 Verifique o valor de
|name-list-format=amp(ajuda) - Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). Feynman Lectures on Physics. Vol. 1. [S.l.]: Addison-Wesley. ISBN 978-0-201-51003-4
- Grøn, Øyvind; Hervik, Sigbjørn (2007). Einstein's General Theory of Relativity. New York: Springer. ISBN 978-0-387-69199-2
- Kutner, Marc (2003). Astronomy: A Physical Perspective . [S.l.]: Cambridge University Press. ISBN 978-0-521-52927-3
- Misner, Charles; Thorne, Kip S.; Wheeler, John Archibald (1973). Gravitation. San Francisco: W. H. Freeman. ISBN 978-0-7167-0344-0
- Peebles, P. J. E. (1993). Principles of Physical Cosmology. [S.l.]: Princeton University Press. ISBN 978-0-691-01933-8
- Taylor, Edwin F.; Wheeler, John Archibald (1992). Spacetime Physics: Introduction to Special Relativity 2nd ed. [S.l.]: W.H. Freeman. ISBN 978-0-7167-2327-1
- Weinberg, Steven (1971). Gravitation and Cosmology. [S.l.]: John Wiley. ISBN 978-0-471-92567-5
- Veja também livros didáticos de cosmologia física para aplicações dos desvios para o vermelho cosmológicos e gravitacionais.
Ligações externas
editar- Ned Wright's Cosmology tutorial
- Cosmic reference guide entry on redshift
- Mike Luciuk's Astronomical Redshift tutorial
- Animated GIF of Cosmological Redshift by Wayne Hu
- Merrifield, Michael; Hill, Richard (2009). «Z Redshift». SIXTψ SYMBΦLS. Brady Haran for the University of Nottingham