Relação de Ghyben–Herzberg

A relação de Ghyben-Herzberg ou lei de Ghyben-Herzberg (por vezes grafado Ghijben-Herzberg) é um modelo matemático que descreve a relação de equilíbrio hidrostático que governa a espessura de água doce num aquífero lenticular, mais conhecido por aquífero basal, formado devido à diferença de densidade entre as massas de água doce e de água salgada numa formação geológica isotrópica, hidraulicamente não confinada e com elevada permeabilidade. A equação descreve descreve a relação entre as águas subterrâneas doces e salgadas em pequenas ilhas ou em regiões costeiras de substrato muito permeável, nas quais a equação de Ghyben-Herzberg é usada para estimar a dimensão da lente de água doce ou para prevenir a intrusão de água salgada durante a construção de captações perto do mar. A equação é baseada no princípio de Arquimedes e foi inicialmente publicada em 1888 por Willem Badon Ghijben, sendo a sua aplicação alargada em 1901 por Alexander Herzberg.

Corte esquemático através da zona terminal de um aquífero basal (ou lenticular), mostrando a forma lenticular que resulta do equilíbrio entre as massas de água doce e salgada descritas pela relação de Ghyben-Herzberg. Os símbolos $h$ e $z$ são os mesmos que aparecem nas equações abaixo.

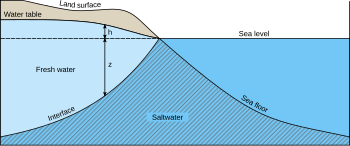
Descrição

A lente de água doce existe em equilíbrio hidrostático com a massa de água salgada, flutuando sobre esta em resultado da menor densidade da água doce e da relativa imiscibilidade que resulta das características do escoamento laminar em meio poroso que ocorre no aquífero.

A relação de equilíbrio entre as massas de água doce e salgada e a dinâmica da intrusão salina em aquíferos isotrópicos foi inicialmente descrita pela formulação proposta por Willem Badon Ghijben em 1888 e 1889, posteriormente aperfeiçoada em 1901 pelo engenheiro berlinense Alexander Herzberg, dando origem à chamada relação de Ghyben–Herzberg (ou lei de Ghyben-Herzberg).

As soluções analíticas derivadas daquela relação descrevem aproximadamente o comportamento da intrusão, mas requerem que seja assumido um conjunto de condições que nem sempre se verificam, o que leva a que os resultados nem sempre modelem correctamente o que é observado.

A relação de Ghyben–Herzberg, representada na figura ao lado, pode ser descrita pela seguinte equação:

$z={\frac {\rho _{f}}{(\rho _{s}-\rho _{f})}}h$

onde a espessura da massa de água doce acima do nível do mar é representada por $h$ e a espessura da mesma massa de água abaixo do nível do mar por $z$. As duas espessuras, $h$ e $z$, estão relacionadas entre si pela rácio entre $\rho _{f}$ e $\rho _{s}$, onde $\rho _{f}$ é a densidade da água doce e $\rho _{s}$ é a densidade da água salgada. Como a água doce tem uma densidade de aproximadamente 1,000 gramas por centímetro cúbico (g/cm³) a 20 °C, enquanto a água salgada tem uma densidade de cerca de 1,025 g/cm³ à mesma temperatura, a equação pode ser simplificada para:

$z\ =40h$.

Nas condições de densidade atrás descritas, admitindo que o material que forma o aquífero é homogéneo e isotrópico na sua condutividade hidráulica, a relação de Ghyben–Herzberg determina que para cada 1 m de elevação da água doce acima do nível do mar existem 40 m de água doce para baixo daquele nível. Esta relação é apenas aproximada, fornecendo um valor indicativo que pode ser refinado recorrendo às modernas técnicas de computação com recurso a métodos numéricos, geralmente diferenças finitas ou elementos finitos, que requerem menor grau de simplificação e podem ser mais facilmente generalizados na sua aplicação.

Admitindo uma densidade da água doce ($\rho _{f}$) de 1,000 kg/l e a da água salgada ($\rho _{s}$) como 1,025 kg/l, um exemplo de aplicação da relação conduz aos seguintes resultados:

$\rho _{\text{f}}=1{,}000g/cm^{3}$.

$\rho _{\text{s}}=1{,}025g/cm^{3}$.

que aplicado na fórmula conduz a:

${\frac {\rho _{\text{f}}}{\rho _{\text{s}}-\rho _{\text{f}}}}={\frac {1}{1{,}025-1}}={\frac {1}{0{,}025}}=40$

pelo que sob as condições usuais da água salgada e de água doce teremos:

$z=40h$,

no entanto, dependendo da salinidade assumida, esse valor pode variar. Cada metro de água doce acima do nível do mar corresponde a aproximadamente 40 metros de água doce abaixo do nível do mar. Por exemplo, se o nível do lençol freático estivar a uma altura de 3 metros acima do nível do mar, num poço próximo ao mar a água seria doce até uma profundidade de $3\cdot 40m=120m$ abaixo do nível médio do mar. Nesse caso, a espessura total da água doce seria: $3m+120m=123m$.

Tendo em conta que a relação de Ghyben-Herzberg é uma manifestação da impulsão arquimediana, a espessura da lentícula de água doce para baixo do nível do mar varia inversamente com o aumento da densidade da água salgada. Como exemplo extremo, veja-se que no caso do Mar Morto, cuja salinidade extrema faz com que a água tenha uma densidade média de: $\rho _{\text{s}}=1{,}240g/cm^{3}$,

de que resulta:

${\frac {\rho _{\text{f}}}{\rho _{\text{s}}-\rho _{\text{f}}}}={\frac {1}{1{,}240-1}}={\frac {1}{0{,}240}}\approx 4{,}15$

pelo que a relação entre a espussura acima e abaixo do nível do mar será:

$h_{\text{oMS}}\approx 4{,}15h$,

ou seja, por cada 1 m de coluna de água doce acima do nível do mar existirá apenas 4,15 m de coluna de água doce abaixo daquele nível, valor quase 10 vezes menor que o verificado em águas com a salinidade média dos oceanos. Repetindo o exemplo anterior, se a superfície freática estiver a 3 m acima do nível médio do mar, a superfície inferior estará a $3\cdot 4{,}15m=12{,}45m$ abaixo do nível médio do mar, pelo que a espessura total da camada de água doce será de apenas: $12{,}45m+3,00m=15{,}45m$.