Tensor de curvatura de Riemann
Em geometria diferencial, tensor de curvatura é uma das noções métricas mais importantes. Um tensor de curvatura é uma generalização da curvatura de Gauss em dimensões mais altas (dois exemplos disto são o tensor de Riemann que se desenvolve neste artigo e o tensor de Ricci).
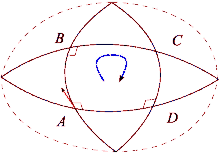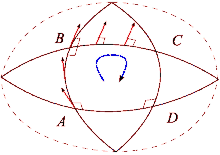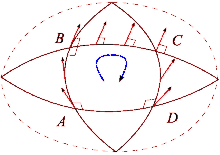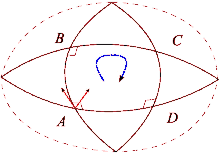
A geometria infinitesimal das variedades de Riemann com dimensão ≥ 3 é demasiado complicada para ser descrita totalmente por um número em um ponto dado (tal como sucede quando a dimensão é menor ou igual a 2). Assim em 2 dimensões a curvatura pode ser representada por um número escalar (ou tensor de ordem zero), em 3 dimensões a curvatura pode ser representada por um tensor de segunda ordem (como por exemplo o tensor de Ricci). Entretanto para dimensões totalmente gerais se necessita ao menos um tensor de quarta ordem (como o tensor de Riemann). Foi Riemann quem introduziu uma maneira de descrever completamente a curvatura em qualquer número de dimensões mediante um "pequeno monstro" de tensor, chamado tensor de Riemann.
Descrição
editarDefinição geral
editarSeja uma variedade diferenciável dotada de uma conexão , definida em um ponto da variedade. O tensor de Riemann é o campo tensorial de tipo (1,3) que satisfaz a igualdade
,
em que são campos vetoriais em , sendo o colchete de Lie dos campos vetoriais. é linear em , de modo que o valor de em só depende dos valores de e em .[1] É importante destacar que o tensor de Riemann é algumas vezes representado pelo sinal oposto.
O teorema de Schwarz afirma que no espaço euclidiano as derivadas parciais comutam: este fato não é verdade em uma variedade com conexão arbitrária, e o tensor de Riemann leva isso em consideração. Então, é possível interpretar o tensor de curvatura de Riemann como o modo de medir o quanto a variedade difere de um espaço euclidiano, ou de um espaço de Minkowski no contexto da relatividade. Logo, um espaço é dito plano quando o tensor de Riemann é zero.
Considerando um sistema de coordenadas , em que e . Então, e portanto a fórmula simplifica como
- ,
ou seja, neste caso o tensor de curvatura mede a não-comutatividade da derivada covariante.[2]
Expressão em coordenadas
editarConsiderando a base coordenada e sua correspondente dual , o tensor de Riemann pode ser expresso como
- ,
em que representa o produto interno.
Deste modo, a expressão pode ser representada em termos de coordenadas usando os símbolos de Christoffel. Valendo-se da convenção do somatório de Einstein, pode-se representá-lo como
- ,
sendo .[3]
Comutadores e índices
editarDado um quadrivetor genérico , o tensor de Riemann surge da comutação da derivada covariante segunda desse quadrivetor, ou seja,[4]
- ,
no qual é o tensor de torção.
Considerando o caso em que não há torção, isto é,
- ,
o tensor de Riemann expressa a diferença medida da curvatura da variedade quando o vetor é transportado do ponto para um ponto , primeiramente ao longo de uma congruência, e depois seguindo outra congruência, ou vice-versa.[5]
Versão covariante
editarO tensor métrico covariante pode se usado para abaixar um índice do tensor de Riemann, assim como o tensor contravariante pode levantar um índice. Assim, a versão completamente covariante do tensor de curvatura do tipo (0,4) é dada por
Propriedades
editarSimetrias algébricas
editarO tensor de Riemann é antissimétrico nos dois últimos índices, ou seja,
- ,
- .
Na sua forma completamente covariante, o tensor de Riemann é antissimétrico em relação à troca dos dois primeiros índices, isto é,
- ,
e é simétrico em relação à troca do primeiro par de índices com o segundo:
- .
Primeira identidade de Bianchi
editarNa ausência de torção, temos:
- .
Esta relação também pode ser escrita mais como
- ,
em que indica uma antissimetrização nos índices. Assim, deve-se efetuar uma soma sobre todas as permutações dos três últimos índices, com um sinal correspondente à paridade da permutação. Resultando em 6 termos, mas que podem ser acoplados em virtude das propriedades algébricas descritas acima.
Componentes independentes
editarEmbora o tensor de Riemann tenha componentes, em que é a dimensão da variedade sobre qual o tensor é definido, as relações descritas anteriormente reduzem este número a componentes independentes. Para duas, três e quatro dimensões, o número de componentes independentes é respectivamente 1, 6 e 20.[6]
Segunda identidade de Bianchi
editarA segunda identidade de Bianchi é parecida com a primeira, mas leva em consideração a derivada covariante do tensor de Riemann. Na ausência de torção, a identidade possui a seguinte forma:
- .
Essa igualdade pode ser escrita de forma mais concisa como[4]
- .
Tensor de curvatura de Ricci
editarO tensor de curvatura de Ricci é a contração do primeiro e terceiro índice do tensor de Riemann.
Referências
- ↑ S. W. Hawking; G. F. R. Ellis (1973). The large scale structure of space-time. [S.l.]: Cambridge University Press. pp. 35–36. ISBN 978-0-521-20016-5
- ↑ Mandredo P. do Carmo (2015). Geometria Riemanniana 5ª ed. Rio de Janeiro: IMPA. pp. 99–104. ISBN 978-852440036-0
- ↑ Mikio Nakahara (2003). Geometry, topology and physics 2ª ed. [S.l.]: CRC Press. pp. 254–255. ISBN 978-14-200-5694-5
- ↑ a b Sean Carroll (2004). Spacetime and Geometry. San Francisco: Addison Wesley. pp. 121–123; 126–128. ISBN 978-11-084-8839-6
- ↑ Luciano Rezzolla; Olindo Zanotti (2013). Relativistic Hydrodynamics. Oxford: Oxford University Press. pp. 41–46. ISBN 978-01-985-2890-6
- ↑ Ray D'Inverno (1992). Introducing Einstein's Relativity. Nova Iorque: Oxford University Press. pp. 86–87. ISBN 0-19-859686-3