O teorema de Papo ,[ 1] teorema de Pappus ,[ 2] Papo (ou Pappus) de Alexandria , é um teorema de geometria projetiva do plano sobre o alinhamento de três pontos:
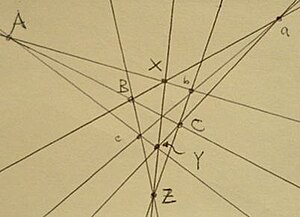
Teorema de Papo: hexágono XbCYcB , cujos lados são formados pelas retas Ab-bC-Ca-aB-Bc-cA, se as retas Xb , BC e cY são concorrentes e se BX , cb e YC são concorrentes, então as retas Bc , XY e bC serão também concorrentesDado um conjunto de pontos colineares A, B, C, e um outro conjunto de pontos colineares a, b, c, os pontos de intersecção x, y, z dos pares de retas Ab- aB, Ac- aC e Bc - bC também serão colineares.
A dualidade desse teorema afirma que:
Dado um conjunto de linhas concorrentes A, B, C, e um outro conjunto de linhas concorrentes a, b, c, então as linhas x, y, z definidas pelos pares de pontos resultantes dos pares de intersecção ( A∩ , a∩ ), ( A∩ , a∩ ) e ( B∩ , b∩ ) são concorrentes .
A generalização deste teorema é o teorema de Pascal , que foi descoberto por Blaise Pascal , quando tinha 16 anos de idade.
editar
Hexágono XbCYcB exemplo do Teorema de Papo Vamos considerar seis linhas em um plano projetado: U , V , W , X , Y , e Z . Então o teorema pode ser expresso como:
Se
(1) os pontos equivalentes as intersecções de U com V , X com W , e Y com Z são colineares,
e se
(2) os pontos equivalentes as intersecções de U com Z , X com V , e Y com W são colineares, então
deve ser verdade que
(3) os pontos equivalentes a intersecções de U com W , X com Z , e Y com V são colineares.
Simbolicamente, o teorema de papus afirma o seguinte:
Se
⟨
U
×
V
,
X
×
W
,
Y
×
Z
⟩
=
0
{\displaystyle \langle U\times V,X\times W,Y\times Z\rangle =0}
e se
⟨
U
×
Z
,
X
×
V
,
Y
×
W
⟩
=
0
{\displaystyle \langle U\times Z,X\times V,Y\times W\rangle =0}
então
⟨
U
×
W
,
X
×
Z
,
Y
×
V
⟩
=
0.
{\displaystyle \langle U\times W,X\times Z,Y\times V\rangle =0.}
Sendo
α
=
⟨
U
×
V
,
X
×
W
,
Y
×
Z
⟩
{\displaystyle \alpha =\langle U\times V,X\times W,Y\times Z\rangle }
β
=
⟨
U
×
Z
,
X
×
V
,
Y
×
W
⟩
{\displaystyle \beta =\langle U\times Z,X\times V,Y\times W\rangle }
γ
=
⟨
U
×
W
,
X
×
Z
,
Y
×
V
⟩
{\displaystyle \gamma =\langle U\times W,X\times Z,Y\times V\rangle }
Nós temos que demonstrar que se
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }
Utilizando a identidade
⟨
A
,
B
,
C
⟩
=
⟨
C
,
A
,
B
⟩
=
⟨
B
,
C
,
A
⟩
{\displaystyle \langle A,B,C\rangle =\langle C,A,B\rangle =\langle B,C,A\rangle }
podemos expressar
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }
α
=
⟨
U
×
V
,
X
×
W
,
Y
×
Z
⟩
{\displaystyle \alpha =\langle U\times V,X\times W,Y\times Z\rangle }
β
=
⟨
Y
×
W
,
U
×
Z
,
X
×
V
⟩
{\displaystyle \beta =\langle Y\times W,U\times Z,X\times V\rangle }
γ
=
⟨
X
×
Z
,
Y
×
V
,
U
×
W
⟩
{\displaystyle \gamma =\langle X\times Z,Y\times V,U\times W\rangle }
Aplicando as propriedades
⟨
A
,
B
,
C
⟩
=
A
⋅
(
B
×
C
)
{\displaystyle \langle A,B,C\rangle =A\cdot (B\times C)}
A
×
(
B
×
C
)
=
(
A
⋅
C
)
B
−
(
A
⋅
B
)
C
{\displaystyle A\times (B\times C)=(A\cdot C)B-(A\cdot B)C}
obtemos
α
=
(
U
×
V
)
⋅
(
(
X
×
W
)
×
(
Y
×
Z
)
)
{\displaystyle \alpha =(U\times V)\cdot ((X\times W)\times (Y\times Z))}
β
=
(
Y
×
W
)
⋅
(
(
U
×
Z
)
×
(
X
×
V
)
)
{\displaystyle \beta =(Y\times W)\cdot ((U\times Z)\times (X\times V))}
γ
=
(
X
×
Z
)
⋅
(
(
Y
×
V
)
×
(
U
×
W
)
)
{\displaystyle \gamma =(X\times Z)\cdot ((Y\times V)\times (U\times W))}
e então
α
=
(
U
×
V
)
⋅
(
⟨
X
,
W
,
Z
⟩
Y
−
⟨
X
,
W
,
Y
⟩
Z
)
{\displaystyle \alpha =(U\times V)\cdot (\langle X,W,Z\rangle Y-\langle X,W,Y\rangle Z)}
β
=
(
Y
×
W
)
⋅
(
⟨
U
,
Z
,
V
⟩
X
−
⟨
U
,
Z
,
X
⟩
V
)
{\displaystyle \beta =(Y\times W)\cdot (\langle U,Z,V\rangle X-\langle U,Z,X\rangle V)}
γ
=
(
X
×
Z
)
⋅
(
⟨
Y
,
V
,
W
⟩
U
−
⟨
Y
,
V
,
U
⟩
W
)
{\displaystyle \gamma =(X\times Z)\cdot (\langle Y,V,W\rangle U-\langle Y,V,U\rangle W)}
Usando a propriedade distributiva do produto escalar :
α
=
⟨
X
,
W
,
Z
⟩
⟨
U
,
V
,
Y
⟩
−
⟨
X
,
W
,
Y
⟩
⟨
U
,
V
,
Z
⟩
{\displaystyle \alpha =\langle X,W,Z\rangle \langle U,V,Y\rangle -\langle X,W,Y\rangle \langle U,V,Z\rangle }
β
=
⟨
U
,
Z
,
V
⟩
⟨
Y
,
W
,
X
⟩
−
⟨
U
,
Z
,
X
⟩
⟨
Y
,
W
,
V
⟩
{\displaystyle \beta =\langle U,Z,V\rangle \langle Y,W,X\rangle -\langle U,Z,X\rangle \langle Y,W,V\rangle }
γ
=
⟨
Y
,
V
,
W
⟩
⟨
X
,
Z
,
U
⟩
−
⟨
Y
,
V
,
U
⟩
⟨
X
,
Z
,
W
⟩
{\displaystyle \gamma =\langle Y,V,W\rangle \langle X,Z,U\rangle -\langle Y,V,U\rangle \langle X,Z,W\rangle }
Com as identidades
⟨
A
,
B
,
C
⟩
=
⟨
C
,
A
,
B
⟩
=
⟨
B
,
C
,
A
⟩
{\displaystyle \langle A,B,C\rangle =\langle C,A,B\rangle =\langle B,C,A\rangle }
⟨
A
,
B
,
C
⟩
=
−
⟨
A
,
C
,
B
⟩
=
−
⟨
C
,
B
,
A
⟩
=
−
⟨
B
,
A
,
C
⟩
{\displaystyle \langle A,B,C\rangle =-\langle A,C,B\rangle =-\langle C,B,A\rangle =-\langle B,A,C\rangle }
Podemos permutar os termos como segue:
α
=
⟨
X
,
W
,
Z
⟩
⟨
U
,
V
,
Y
⟩
−
⟨
X
,
W
,
Y
⟩
⟨
U
,
V
,
Z
⟩
{\displaystyle \alpha =\langle X,W,Z\rangle \langle U,V,Y\rangle -\langle X,W,Y\rangle \langle U,V,Z\rangle }
β
=
−
⟨
U
,
Z
,
X
⟩
⟨
Y
,
W
,
V
⟩
+
⟨
X
,
W
,
Y
⟩
⟨
U
,
V
,
Z
⟩
{\displaystyle \beta =-\langle U,Z,X\rangle \langle Y,W,V\rangle +\langle X,W,Y\rangle \langle U,V,Z\rangle }
γ
=
⟨
U
,
Z
,
X
⟩
⟨
Y
,
W
,
V
⟩
−
⟨
X
,
W
,
Z
⟩
⟨
U
,
V
,
Y
⟩
{\displaystyle \gamma =\langle U,Z,X\rangle \langle Y,W,V\rangle -\langle X,W,Z\rangle \langle U,V,Y\rangle }
Agora podemos somar as equações para obter:
α
+
β
+
γ
=
0
{\displaystyle \alpha +\beta +\gamma =0}
γ
=
−
(
α
+
β
)
{\displaystyle \gamma =-(\alpha +\beta )}
de onde segue que se
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
γ
{\displaystyle \gamma }