Trapézio (geometria)
Na geometria o trapézio é um quadrilátero com dois lados paralelos entre si, que são chamados de base maior e base menor.
| Trapézio (geometria) | |
|---|---|
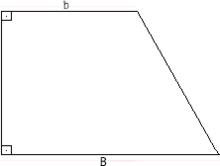 Trápezio retângulo | |
| Arestas e Vértices | 4 |
| Área | |
Definição
editarA definição mais aceita para um trapézio é a seguinte:
Um quadrilátero plano convexo é um trapézio se, e somente se, possui dois lados paralelos.[1]
Alguns autores[2] definem um trapézio como sendo um quadrilátero que possui exatamente um par de lados paralelos, excluindo portanto os paralelogramos, porém essa definição não é a mais rigorosa existente, pois ela faria com que conceitos tais como o da aproximação trapezoidal para a integral definida fossem mal definidos. Para tanto, admite-se a definição vista acima.[3]
Propriedades dos trapézios
editarOs trapézios possuem as seguintes propriedades:[1]
- Em qualquer trapézio de bases e temos que .
- Os ângulos de cada base de um trapézio isósceles são congruentes.
- As diagonais de um trapézio isósceles são congruentes.
Demonstração das propriedades
editar1º Propriedade
editarEm qualquer trapézio de bases e temos que
, é transversal
e
, é transversal
Logo temos que
2° Propriedade
editarOs ângulos de cada base de um trapézio isósceles são congruentes
Para demonstrar essa propriedade vamos, primeiro, enunciá-la matematicamente.
Tomando dois pontos e , de modo que ambos estejam em e que e .
Como é um trapézio nós sabemos que , o que implica que , por serem distâncias entre retas paralelas.
Se observarmos os triângulos e , podemos ver que eles são congruentes:
Como os triângulos são congruentes, temos que .
Por fim, visto que e são suplementares de e , respectivamente (por conta da propriedade demonstrada anteriormente), temos: .
Logo os ângulos de cada base de um trapézio isósceles são congruentes.
3º Propriedade
editarAs diagonais de um trapézio isósceles são congruentes.
Para demonstrar essa propriedade vamos, primeiramente, enunciá-la matematicamente.
Observe os triângulos e , que são congruentes:
Sabendo que os triângulos são congruentes temos:
Logo as diagonais de um trapézio isósceles são congruentes.
Cálculo da área
editarA área A de um trapézio simples (isto é, sem auto-interseções) é dada por[3]
em que B e b são os comprimentos dos lados paralelos (as bases maior e menor) e h é a altura (a distância entre esses lados). Em 499 EC Aryabhata, um grande matemático-astrônomo da era clássica da matemática e física indiana, usou este método no Ariabatiia (seção 2.8).[4] A fórmula anterior tem como caso particular a fórmula que fornece a área de um triângulo, considerando-se um triângulo como um trapézio degenerado em que um dos lados paralelos foi reduzido a um único ponto.
A mediana do trapézio é o segmento que une os pontos médios dos lados não paralelos. O seu comprimento m é igual à média dos comprimentos das bases do trapézio:
Consequentemente, a área do trapézio é calculada pela multiplicação de sua mediana por sua altura:
O lado de um trapézio retângulo pode ser calculado pela formula:
Referências
- ↑ a b Dolce, Osvaldo (2013). Fundamentos de Matemática Elementar 9: Geometria plana. [S.l.]: Atual
- ↑ «American School definition from "math.com"». Consultado em 14 de abril de 2008
- ↑ a b Weisstein, Eric W. «Trapezoid». MathWorld (em inglês)
- ↑ Aryabhatiya Arquivado em 2011-08-15 na Archive.today em marata: आर्यभटीय, Mohan Apte, Pune, India, Rajhans Publications, 2009, p.66, ISBN 978-81-7434-480-9

