Conjunto conexo

Conjunto conexo, em Teoria dos conjuntos numéricos, é o que não pode ser dividido em apenas dois subconjuntos fechados que não tenham nenhum ponto comum. Ou seja, podemos dizer que um espaço é conexo se pode passar de um ponto qualquer deste espaço para qualquer outro ponto distinto por um movimento contínuo, sem sair dele.

	Letras i e j minúsculas, com pontos em vermelho
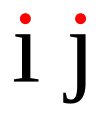
Espaço conexo	Dois espaços desconexos (é impossível ir da letra propriamente dita até o ponto sem sair do espaço)

Definição

Mais formalmente podemos definir conjunto conexo da seguinte forma: Diz-se que um conjunto E em um espaço métrico X é conexo se não existem em X dois subconjuntos A e B abertos e disjuntos tais que $A\cap E\neq \emptyset$, $B\cap E\neq \emptyset$ e $E\subset A\cup B$.

Também pode-se definir conjunto desconexo, sendo este um conjunto E que satisfaz às seguintes condições:

• $E=E_{1}\cup E_{2}$ com $E_{1}$ e $E_{2}$ não vazios
• ${\bar {E_{1}}}\cap E_{2}=\emptyset$
• $E_{1}\cap {\bar {E_{2}}}=\emptyset$

Nesse caso um conjunto é dito conexo quando ele não é desconexo. Lembramos aqui que a notação ${\bar {A}}$ representa o fecho do conjunto A.

Faz sentido também falarmos de espaços conexos, sendo estes espaços que não são a reunião de dois conjuntos abertos disjuntos não vazios, ou seja, um espaço é conexo se admite apenas cisão trivial.

Teoremas

Teorema 1

Dados dois conjuntos B e C, então ${\bar {B}}\cap C={\bar {C}}\cap B=\emptyset$ se e somente se existem F e G abertos tais que $B\subset F$, $C\subset G$ e $F\cap G=\emptyset$.

Teorema 2

Um subconjunto E da reta real $\mathbb {R}$ é conexo se, e somente se, E tem a seguinte propriedade: Se $x\in E$, $y\in E$ e $x<z<y$, então $z\in E$.

Corolário

Todo os conjuntos conexos da reta são intervalos.

Teorema 3

A imagem de um conjunto conexo por uma aplicação contínua é um conjunto conexo (é um invariante topológico).

Teorema 4

O fecho de um conjunto conexo é conexo.

Teorema 5

O produto cartesiano de espaços métricos $M=M_{1}\times \cdots \times M_{n}$é conexo se, e somente se, cada fator $M_{i}$ é conexo.

Exemplos e observações

• O cilindro C={${(x,y,z)\in \mathbb {R} ^{3}:x^{2}+y^{2}=1}$} é homeomorfo ao produto cartesiano $[0,2\pi )\times (\infty ,-\infty )$. Como $[0,2\pi )\times (\infty ,-\infty )$ são intervalos, eles são conexos; portanto, o produto cartesiano é conexo e a imagem C de uma aplicação homeomórfica é também um conjunto conexo. Conclui-se, então, que C é um conjunto conexo.
• Um conjunto conexo, se for complementarmente conjunto compacto, definirá um conjunto contínuo.
• Os conjuntos $\mathbb {N} ,\mathbb {Z}$ e $\mathbb {Q}$ são desconexos.

Ver também

• Conjunto compacto
• Conjunto contínuo
• Continuidade
• Números reais