Distância Hausdorff
Na matemática, a Distância Hausdorff, ou métrica Hausdorff, também chamado de Distância Pompeiu-Hausdorff, mede o quão distante dois subconjuntos do espaço de metrica estão um do outro. [1]
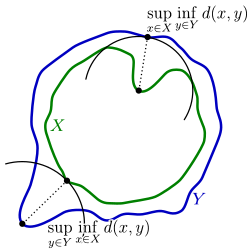
De modo informal, dois conjuntos estão pertos, do ponto de vista da distância Hausdorff, se todo ponto de cada conjunto está perto a algum ponto do outro conjunto. A Distância Hausdorff é a maior distância que pode ser forçado a trafegar por um adversário que escolhe um ponto de um dos dois conjuntos, de onde você então deve viajar até o outro conjunto. Em outras palavras, é o mais distante ponto de um conjunto que você pode estar para um ponto próximo de um conjunto diferente.
Definição
editarSeja X e Y dois subconjuntos não vazios de um espaço métrico (M, d). Nós definimos a distância Hausdorff d H(X, Y) por:
Aplicações
editarEm visão computacional, a distância Hausdorff pode ser usadas para encontrar uma dada estrutura numa imagem alvo. A estrutura dada e a imagem são frequentemente pré-processados para detecção de bordas. Então cada ponto ativo nas duas imagens são tratados como pontos de um conjunto, representando o formato. O algoritmo tenta então minimizar a distância Hausdorff entre os dois conjuntos, assim a parte da imagem com o menor valor de distância pode ser considerada a estrutura procurada.[2]
Em computação gráfica, essa medida de distância pode ser usadas para medir a distância entre duas representações do mesmo objeto 3D[3] particularmente quando se procura um nível de detalhe ideal para apresentação eficiente de modelos 3D complexos.
Referências
- ↑ Hausdorff metric -- PlanetMath
- ↑ Hausdorff-Based Matching
- ↑ P. Cignoni, C. Rocchini, R. Scopigno, "Metro: Measuring Error on Simplified Surfaces", Computer Graphics Forum, Volume 17, Number 2, June 1998, pp. 167-174