Reflexão (matemática)
Em Matemática ou, mais precisamente, em geometria, reflexão é uma transformação geométrica do ponto, da reta, do plano ou do espaço que "espelha" todos os pontos em relação, respectivamente, a um ponto (dito centro de reflexão), uma reta (dita eixo de reflexão ou eixo de simetria) [1][2][3]ou um plano (chamado plano de reflexão ou de simetria), transformando o ponto, a reta ou o plano num outro, que lhe é simétrico em relação ao eixo dado.

Uma reflexão do plano euclidiano é uma simetria ortogonal em relação a uma reta (reta vetorial, quando se tratar de um plano vetorial euclidiano). Portanto, uma reflexão constitui uma simetria axial ortogonal.
Em geral, dentro de um espaço euclidiano qualquer, uma reflexão é uma simetria ortogonal em relação a um hiperplano, isto é, a um subespaço de codimensão 1. Em dimensão 3, trata-se portanto de uma simetria ortogonal em relação a um plano.
As reflexões, como todas as simetrias, são transformações involutivas.
O termo se remete originalmente aos espelhos, que refletem uma imagem. A figura imagem e a figura original são biométricas.
Reflexo em torno de uma reta
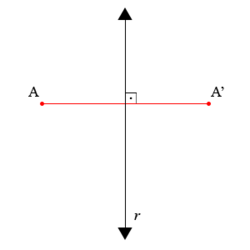
editarA reflexão em torno de uma reta também é conhecida como simetria axial.
Seja r uma reta no plano π. A reflexão em torno da reta r é a transformação:
: π → π
assim definida.
ρ(x)=x
que associa,a cada ponto x do plano, o ponto x’, tal que r é a mediatriz do segmento xx’. [4]
Assim, reflexão de um objeto em torno de uma reta r é o movimento que transforma cada ponto A em outro ponto Sr(A)=A' da imagem.
Construção geométrica
editarPodemos construir o ponto simétrico utilizando-se de régua e compasso:
- Com a ponta seca(do compasso) em qualquer ponto da reta e raio igual à distância entre o ponto escolhido e A, trace uma circunferência;
- Repita o procedimento com outro ponto da reta;
- As duas circunferências irão se encontrar em dois pontos. Um deles é A, o outro é o seu simétrico. Na reflexão, um ponto e a sua imagem estão à mesma distancia do eixo de reflexão.
Referências
- ↑ Reflexão em torno da reta y = x
- ↑ Reflexão em torno do eixo y
- ↑ Reflexão em torno do eixo x
- ↑ LIRA, Ana C. B. A matemática dos espelhos: proposta para o ensino-aprendizagem de matrizes utilizando transformações geométricas". Arquivado em 2 de abril de 2015, no Wayback Machine. Campina Grande: Universidade Estadual da Paraíba, 2011; p. 8s
Ver também
editarLigações externas
editar- UFRJ. Projeto Novas Tecnologias no Ensino. Introdução às funções reais. Módulo I. Capítulo II - "Coordenadas e Transformações no Plano. Reflexões Axiais".