Volta (geometria)
Uma volta (símbolo tr, pla ou N) é uma unidade de medida de ângulo plano que é igual a 2π radianos, 360 graus ou 400 grados. Assim, é a medida angular subentendida por uma circunferência completa no seu centro. Como uma unidade angular, uma volta também corresponde a um ciclo (símbolo c)[1] ou a uma rotação (símbolo rot ou r).[2] Unidades de frequência frequentemente relacionadas são ciclos por segundo (cps) e rotações por minuto (rpm). A unidade angular de volta é útil quando relacionadas com enrolamentos (por exemplo, transformadores), objetos girando, índice de curvas, entre outros.
No ISQ, um "número de voltas" arbitrário (também conhecido como "número de rotações" ou "número de ciclos") é formalizado como uma grandeza adimensional chamada rotação, definida como a razão de um dado ângulo e sua volta completa. É representado pelo símbolo N. (Ver abaixo para a fórmula.) Subdivisões de uma volta incluem meia volta e um quarto de volta, abrangendo uma ângulo raso e um ângulo reto, respectivamente; prefixos métricos também podem ser utilizados, como em centivolta e milivolta, por exemplo.
Outra unidade comum para representar ângulos é o radiano, que geralmente é expresso em termos de π (pi). O símbolo π, que representa meia volta, foi desenvolvido por William Jones em 1706 e depois popularizado por Leonhard Euler.[3][4] Em 2010, Michael Hartl propôs usar em vez disso o símbolo τ (tau), igual a 2π e correspondendo a uma volta completa, para uma maior simplicidade conceitual.[5] Essa proposta inicialmente não obteve ampla aceitação na comunidade matemática,[6] mas a constante se tornou mais difundida,[7] tendo sido adicionada a várias linguagens de programação e calculadoras importantes.
Símbolos da unidade
editar"N" nas unidades do ISQ e do SI
editarUm conceito relacionado à unidade angular "volta", definida pelo Sistema Internacional de Grandezas (ISQ) e adotada no Sistema Internacional de Unidades (SI), é a grandeza física volta (símbolo N), definida como o número de rotações:[8]
N é o número (não necessáriamente inteiro) deo rotações, por exemplo, de um corpo em rotação de um dado eixo. Seu valor é dado por:
- N = φ2π rad
onde φ denota a medida da posição angular.
A definição acima faz parte do ISQ, formalizado no padrão internacional ISO 80000-3 (espaço e tempo),[8] e adotado no SI.[9][10] No ISQ/SI, a rotação é usada para derivar a frequência de rotação, n=dN/dt, com a unidade base do SI do inverso do segundo (s-1); Unidades de frequência relacionadas comuns são hertz (Hz), ciclos por segundo (cps) e rotações por minuto (rpm).
A versão obsoleta ISO 80000-3:2006 definiu "rotação" como um nome especial para a grandeza adimensional "um",[a] que também recebeu outros nomes especiais, como o radiano.[b] Apesar de sua homogeneidade dimensional, essas duas unidades adimensionais especialmente nomeadas são aplicáveis para tipos de grandeza não comparáveis: rotação e ângulo, respectivamente.[12] "Ciclo" também é mencionado na ISO 80000-3, na definição de período.[c]
"pla" na UE e na Suiça
editarO padrão alemão DIN 1315 (março de 1974) propôs o símbolo da unidade "pla" (do latim: plenus angulus, "ângulo completo") para voltas.[13][14] Abordado no DIN 1301-1 (outubro de 2010), o chamado Vollwinkel ("ângulo completo") não é uma unidade do SI. No entanto, é uma unidade de medida legal na União Europeia[15][16] e na Suíça.[17]
"tr" nas calculadoras
editarAs calculadoras científicas HP 39gII e HP Prime suportam o símbolo de unidade "tr" para voltas desde 2011 e 2013, respectivamente. O suporte para "tr" também foi adicionado ao newRPL para a HP 50g em 2016 e para a hp 39g+, HP 49g+, HP 39gs e HP 40gs em 2017.[18][19] Um modo angular TURN também foi sugerido para o WP 43S,[20] mas a calculadora implementa "MULπ" (múltiplos de π) como modo e unidade desde 2019.[21] [22]
Propostas para uma única letra representar 2π
editarO significado do símbolo π não foi originalmente fixado à razão entre o comprimento da circunferência e o diâmetro. Em 1697, David Gregory usou πρ (pi sobre rô) para denotar o perímetro de uma circunferência dividida pelo seu raio.[23][24] No entanto, anteriormente, em 1647, William Oughtred havia usado δπ (delta sobre pi) para a razão entre o diâmetro e o perímetro. O primeiro uso do símbolo π por si só com seu significado atual (perímetro dividido pelo diâmetro) foi em 1706 pelo matemático galês William Jones.[25] Euler então adotou o símbolo com esse significado, levando ao seu uso generalizado.[3]
Em 2001, Robert Palais propôs usar o número de radianos em uma volta como a constante de círculo fundamental em vez de π, o que equivale ao número de radianos em meia volta, para tornar a matemática mais simples e intuitiva. Sua proposta utilizava um símbolo de "π com três pernas" para denotar a constante ( ).[26]
Em 2008, Thomas Colignatus propôs o uso da letra grega maiúscula teta, Θ, para representar 2π.[27] A letra grega teta deriva da letra fenícia e hebraica tete, 𐤈 ou ט, e observa-se que a versão mais antiga do símbolo, que significa roda, se assemelha a uma roda com quatro raios.[28] Também foi proposto o uso do símbolo de roda, tete, para representar o valor 2π, e mais recentemente foi estabelecida uma conexão entre outras culturas antigas sobre a existência de um símbolo de roda, sol, círculo ou disco — ou seja, outras variações de tete — como representação para 2π.[29]
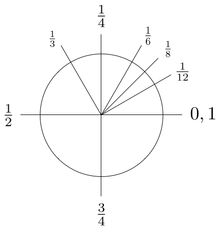
Em 2010, Michael Hartl propôs usar a letra grega tau para representar a constante da circunferência: τ = 2π. Ele ofereceu duas razões. Primeiro, τ é o número de radianos em uma volta, o que permite expressar frações de uma volta de forma mais direta: por exemplo, 34 de uma volta seria representada como 3τ4 rad em vez de 3τ4 rad. Segundo, τ se assemelha visualmente a π, cuja associação com a constante da circunferência é inevitável.[5] O Manifesto Tau[30] de Hartl fornece muitos exemplos de fórmulas consideradas mais claras quando τ é usado em vez de π,[31][32][33] como uma associação mais estreita com a geometria da identidade de Euler usando eiτ = 1 em vez de eiπ = −1.
Inicialmente, nenhuma dessas propostas recebeu ampla aceitação pelas comunidades matemáticas e científicas.[6] No entanto, o uso de τ tornou-se mais difundido.[7] Por exemplo:
- Em 2012, o site educacional Khan Academy começou a aceitar respostas expressas em termos de τ.[34]
- A constante τ foi disponibilizada na calculadora do Google, na calculadora gráfica Desmos[35] e em várias linguagens de programação, como Python,[36][37] Raku,[38] Processing,[39] Nim,[40] Rust,[41] GDScript,[42] UE Blueprints,[43] Java,[44][45] e .NET.[46][47]
- Também foi utilizada em pelo menos um artigo de pesquisa matemática,[48] escrito pelo defensor de τ Peter Harremoës.[49]
A seguinte tabela apresenta com várias identidades aparecem quando τ = 2π é utilizado em vez de π.[26][50] Para uma lista mais completa, veja Lista de fórmulas envolvendo π.
| Fórmula | Usando π | Usando τ | Notas |
|---|---|---|---|
| Ângulo subtendido em 14 de uma circunferência | π2 rad | τ4 rad | τ4 rad = 14 de volta |
| Comprimento C de uma circunferência de raio r | C = 2πr | C = τr | |
| Área de um círculo | A = πr2 | A = τ r22 | A área de um setor de ângulo θ é A = θ r22. |
| Área de um polígono regular de n lados com circunraio unitário | A = n2 sin 2πn | A = n2 sin τn | |
| Relação de recorrência entre os volumes de uma n-bola e uma n-esfera | Vn(r) = rn Sn−1(r) Sn(r) = 2πr Vn−1(r) | Vn(r) = rn Sn−1(r) Sn(r) = τr Vn−1(r) | V0(r) = 1 S0(r) = 2 |
| Fórmula integral de Cauchy | |||
| Distribuição normal padrão | |||
| Fórmula de Stirling | |||
| Identidade de Euler | eiπ = −1 eiπ + 1 = 0 |
eiτ = 1 eiτ − 1 = 0 |
Para qualquer inteiro k, eikτ = 1 |
| raízes n-ésimas da unidade | |||
| Constante de Planck | ħ é a constante reduzida de Planck. | ||
| Frequência angular |
Subdivisões
editarUma volta pode ser dividida em 100 centivoltas ou 1000 millivoltas, sendo que cada millivolta corresponde a um ângulo de 0,36°, que também pode ser escrito como 21′ 36″.[51][52] Um transferidor dividido em centiturnos é normalmente chamado de "transferidor de porcentagem".
Embora os transferidores de porcentagem existam desde 1922,[53] os termos centivoltas, millivoltas e microvoltas foram introduzidos muito mais tarde pelo astrônomo britânico Fred Hoyle em 1962.[51][52] Alguns dispositivos de medição para artilharia e observação de satélites possuem millivoltas como escala.[54][55]
Frações binárias de uma volta também são usadas. Tradicionalmente, marinheiros dividiam uma volta em 32 pontos subcolaterais, que implicitamente têm uma separação angular de 1/32 de volta. O grau binário, também conhecido como radiano binário (ou brad), é 1256 de volta.[56] O grau binário é usado em computação para um ângulo poder ser representado com a máxima precisão possível em um único byte. Outras medidas de ângulo usadas em computação podem ser baseadas na divisão de uma volta inteira em 2n partes iguais para outros valores de n.[57]
Conversão de unidade
editarUma volta é igual a 2π (≈ 6.283185307179586)[58] radianos, 360 graus, ou 400 grados.
| Voltas | Radianos | Graus | grados | |
|---|---|---|---|---|
| 0 volta | 0 rad | 0° | 0g | |
| 172 de volta | τ72 rad[d] | π36 rad | 5° | 55g |
| 124 de volta | τ24 rad | π12 rad | 15° | 162g |
| 116 de volta | τ16 rad | π8 rad | 22.5° | 25g |
| 112 de volta | τ12 rad | π6 rad | 30° | 331g |
| 110 de volta | τ10 rad | π5 rad | 36° | 40g |
| 18 de volta | τ8 rad | π4 rad | 45° | 50g |
| 12π de volta | 1 rad | c. 57.3° | c. 63.7g | |
| 16 de volta | τ6 rad | π3 rad | 60° | 662g |
| 15 de volta | τ5 rad | 2π5 rad | 72° | 80g |
| 14 de volta | τ4 rad | π2 rad | 90° | 100g |
| 13 de volta | τ3 rad | 2π3 rad | 120° | 1331g |
| 25 de volta | 2τ5 rad | 4π5 rad | 144° | 160g |
| 12 de volta | τ2 rad | π rad | 180° | 200g |
| 34 de volta | 3τ4 rad | 3π2 rad | 270° | 300g |
| 1 volta | τ rad | 2π rad | 360° | 400g |
Ver também
editarNotas e referências
Notas
- ↑ "O nome especial rotação, símbolo r, para esta unidade [nome 'um', símbolo '1'] é ambplamente utilizado em especificações de máquinas rotatórias."[11]
- ↑ "As unidades de medida de quantidades de dimensão um são números. Em alguns casos, estas unidades de medida recebem nomes especiais, por exemplo, radiano..."[11]
- ↑ "3-14) duração do período, período: duração (item 3-9) de um ciclo de um evento periódico"[8]
- ↑ Nesta tabela, 𝜏 denota 2π.
- Este artigo foi inicialmente traduzido, total ou parcialmente, do artigo da Wikipédia em inglês cujo título é «Turn (angle)», especificamente desta versão.
Referências
- ↑ Fitzpatrick, Richard (2021). Newtonian Dynamics: An Introduction. [S.l.]: CRC Press. p. 116. ISBN 978-1-000-50953-3. Consultado em 25 de abril de 2023
- ↑ Units & Symbols for Electrical & Electronic Engineers (PDF). Londres, Reino Unido: Institution of Engineering and Technology. 2016. Consultado em 18 de julho de 2023. Cópia arquivada (PDF) em 18 de julho de 2023
- ↑ a b «Pi». Encyclopaedia Brittanica (em inglês). 14 de março de 2024. Consultado em 26 de março de 2024
- ↑ Euler, Leonhard (1746). Nova theoria lucis et colorum. Opuscula varii argumenti (em latim). [S.l.]: sumtibus Ambr. Haude & Jo. Carol. Speneri, bibliop. p. 200
- ↑ a b Hartl, Michael (14 de março de 2019) [2010-03-14]. «The Tau Manifesto». Consultado em 14 de setembro de 2013. Cópia arquivada em 28 de junho de 2019
- ↑ a b «Life of pi in no danger – Experts cold-shoulder campaign to replace with tau». Telegraph India. 30 de junho de 2011. Consultado em 5 de agosto de 2019. Arquivado do original em 13 de julho de 2013
- ↑ a b McMillan, Robert (13 de março de 2020). «For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day» . Wall Street Journal (em inglês). ISSN 0099-9660. Consultado em 21 de maio de 2020
- ↑ a b c «ISO 80000-3:2019 Quantities and units — Part 3: Space and time» 2 ed. International Organization for Standardization. 2019. Consultado em 23 de outubro de 2019 [1] (11 pages)
- ↑ Le Système international d’unités (PDF), ISBN 978-92-822-2272-0 (em francês e inglês) 9.ª ed. , International Bureau of Weights and Measures, 2019
- ↑ Thompson, Ambler; Taylor, Barry N. (4 de março de 2020) [2 de julho de 2009]. «The NIST Guide for the Use of the International System of Units, Special Publication 811» 2008 ed. National Institute of Standards and Technology. Consultado em 17 de julho de 2023 [2]
- ↑ a b «ISO 80000-3:2006». ISO. 31 de agosto de 2001. Consultado em 25 de abril de 2023
- ↑ «ISO 80000-1:2009(en) Quantities and units — Part 1: General». iso.org. Consultado em 12 de maio de 2023
- ↑ German, Sigmar; Drath, Peter (13 de março de 2013) [1979]. Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik (em alemão) 1 ed. [S.l.]: Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reimpreção: Springer-Verlag. p. 421. ISBN 978-3-32283606-9. 978-3-528-08441-7, 978-3-32283606-9. Consultado em 14 de agosto de 2015
- ↑ Kurzweil, Peter (9 de março de 2013) [1999]. Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik (em alemão) 1 ed. [S.l.]: Vieweg, reimpreção: Springer-Verlag. p. 403. ISBN 978-3-32292920-4. doi:10.1007/978-3-322-92920-4. 978-3-322-92921-1. Consultado em 14 de agosto de 2015
- ↑ «Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG» (em alemão). 15 de fevereiro de 1980. Consultado em 6 de agosto de 2019. Cópia arquivada em 22 de junho de 2019
- ↑ «Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR)» (em alemão). 11 de março de 2009. Consultado em 6 de agosto de 2019. Cópia arquivada em 6 de agosto de 2019
- ↑ «Art. 15 Einheiten in Form von nichtdezimalen Vielfachen oder Teilen von SI-Einheiten». Einheitenverordnung. Der Bundesrat - Das Portal der Schweizer Regierung (em alemão). [S.l.]: Schweizerischer Bundesrat. 23 de novembro de 1994. 941.202. Consultado em 1 de janeiro de 2013. Cópia arquivada em 10 de maio de 2019
- ↑ Lapilli, Claudio Daniel (11 de maio de 2016). «RE: newRPL: Handling of units». HP Museum. Consultado em 5 de agosto de 2019. Cópia arquivada em 10 de agosto de 2017
- ↑ Lapilli, Claudio Daniel (25 de outubro de 2018). «Chapter 3: Units - Available Units - Angles». newRPL User Manual. hpgcc3. [S.l.: s.n.] Consultado em 7 de agosto de 2019. Cópia arquivada em 6 de agosto de 2019
- ↑ Paul, Matthias R. (12 de janeiro de 2016) [2016-01-11]. «RE: WP-32S in 2016?». HP Museum. Consultado em 5 de agosto de 2019. Cópia arquivada em 5 de agosto de 2019.
[…] I'd like to see a TURN mode being implemented as well. TURN mode works exactly like DEG, RAD and GRAD (including having a full set of angle unit conversion functions like on the WP 34S), except for that a full circle doesn't equal 360 degree, 6.2831... rad or 400 gon, but 1 turn. (I […] found it to be really convenient in engineering/programming, where you often have to convert to/from other unit representations […] But I think it can also be useful for educational purposes. […]) Having the angle of a full circle normalized to 1 allows for easier conversions to/from a whole bunch of other angle units […]
- ↑ Bonin, Walter (2019) [2015]. WP 43S Owner's Manual (PDF). Col: 0.12 draft ed. [S.l.: s.n.] pp. 72, 118–119, 311. ISBN 978-1-72950098-9. Consultado em 5 de agosto de 2019. Cópia arquivada (PDF) em 18 de julho de 2023 [3] [4]
- ↑ Bonin, Walter (2019) [2015]. WP 43S Reference Manual (PDF). Col: 0.12 draft ed. [S.l.: s.n.] pp. iii, 54, 97, 128, 144, 193, 195. ISBN 978-1-72950106-1. Consultado em 5 de agosto de 2019. Cópia arquivada (PDF) em 18 de julho de 2023 [5] [6]
- ↑ Beckmann, Petr (1989) [1970]. A History of Pi. [S.l.]: Barnes & Noble Publishing
- ↑ Schwartzman, Steven (1994). The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English . [S.l.]: The Mathematical Association of America. p. 165. ISBN 978-0-88385511-9
- ↑ Veling, Anne (2001). «Pi through the ages». veling.nl. Arquivado do original em 2 de julho de 2009
- ↑ a b Palais, Robert (2001). «Pi is Wrong» (PDF). New York, USA: Springer-Verlag. The Mathematical Intelligencer. 23 (3): 7–8. doi:10.1007/bf03026846. Consultado em 5 de agosto de 2019. Cópia arquivada (PDF) em 18 de julho de 2019
- ↑ Cool, Thomas "Colignatus" (18 de julho de 2008) [2008-04-08, 2008-05-06]. «Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur» (PDF). Consultado em 18 de julho de 2023. Cópia arquivada (PDF) em 18 de julho de 2023
- ↑ Mann, Steve; Janzen, Ryan E.; Ali, Mir Adnan; Scourboutakos, Pete; Guleria, Nitin (22–24 de outubro de 2014). «Integral Kinematics (Time-Integrals of Distance, Energy, etc.) and Integral Kinesiology». Toronto, Ontario, Canada. Proceedings of the 2014 IEEE GEM: 627–629. Consultado em 18 de julho de 2023
- ↑ Mann, Steve; Chen, Hongyu; Aylward, Graeme; Jorritsma, Megan; Mann, Christina; Defaz Poveda, Diego David; Pierce, Cayden; Lam, Derek; Stairs, Jeremy; Hermandez, Jesse; Li, Qiushi; Xiang, Yi Xin; Kanaan, Georges (junho de 2019). «Eye Itself as a Camera: Sensors, Integrity, and Trust». The 5th ACM Workshop on Wearable Systems and Applications (Keynote): 1–2. doi:10.1145/3325424.3330210. Consultado em 18 de julho de 2023
- ↑ Hartl, Michael (14 de março de 2010). «The Tau Manifesto» (PDF). Consultado em 5 de agosto de 2019. Cópia arquivada (PDF) em 18 de julho de 2019
- ↑ Aron, Jacob (8 de janeiro de 2011). «Michael Hartl: It's time to kill off pi». New Scientist. Interview. 209 (2794): 23. Bibcode:2011NewSc.209...23A. doi:10.1016/S0262-4079(11)60036-5
- ↑ Landau, Elizabeth (14 de março de 2011). «On Pi Day, is 'pi' under attack?». cnn.com. CNN. Consultado em 5 de agosto de 2019. Cópia arquivada em 19 de dezembro de 2018
- ↑ Bartholomew, Randyn Charles (25 de junho de 2014). «Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful». Scientific American. Consultado em 20 de março de 2015. Cópia arquivada em 18 de junho de 2019
- ↑ «Happy Tau Day!». blog.khanacademy.org (em inglês). 28 de junho de 2012. Consultado em 19 de dezembro de 2020. Cópia arquivada em 18 de julho de 2023
- ↑ «Supported Functions». help.desmos.com. Consultado em 21 de março de 2023. Cópia arquivada em 26 de março de 2023
- ↑ Coghlan, Nick (25 de fevereiro de 2017). «PEP 628 -- Add math.tau». Python.org. Consultado em 5 de agosto de 2019. Cópia arquivada em 22 de julho de 2019
- ↑ «math — Mathematical functions». Python 3.7.0 documentation. Consultado em 5 de agosto de 2019. Cópia arquivada em 29 de julho de 2019
- ↑ «Perl 6 terms». Consultado em 5 de agosto de 2019. Cópia arquivada em 22 de julho de 2019
- ↑ «TAU». Processing. Consultado em 5 de agosto de 2019. Cópia arquivada em 22 de julho de 2019
- ↑ «math». Nim. Consultado em 5 de agosto de 2019. Cópia arquivada em 22 de julho de 2019
- ↑ «std::f64::consts::TAU - Rust». doc.rust-lang.org. Consultado em 9 de outubro de 2020. Cópia arquivada em 18 de julho de 2023
- ↑ «Constants @GDScript - Godot Engine (stable) documentation in English». Godot Docs
- ↑ «Get TAU - Unreal Engine 5.2 Documentation». Unreal Engine Docs
- ↑ Darcy, Joe. «JDK-8283136: Add constant for tau to Math and StrictMath». bugs.openjdk.org
- ↑ «Math class». Java 19 documentation
- ↑ John-H-K. «Add Math.Tau Pull Request #37517 · dotnet/Runtime». GitHub
- ↑ «Math.Tau Field». .NET Reference Documentation
- ↑ Harremoës, Peter (2017). «Bounds on tail probabilities for negative binomial distributions». Kybernetika. 52 (6): 943–966. arXiv:1601.05179 . doi:10.14736/kyb-2016-6-0943
- ↑ Harremoës, Peter (17 de novembro de 2018). «Al-Kashi's constant τ» (PDF). Consultado em 20 de setembro de 2018. Cópia arquivada (PDF) em 22 de julho de 2019
- ↑ Abbott, Stephen (abril de 2012). «My Conversion to Tauism» (PDF). Math Horizons. 19 (4): 34. doi:10.4169/mathhorizons.19.4.34. Cópia arquivada (PDF) em 28 de setembro de 2013
- ↑ a b Hoyle, Fred (1962). Chandler, M. H., ed. Astronomy 1 ed. Londres, Reino Unido: Macdonald & Co. (Publishers) Ltd. / Rathbone Books Limited. LCCN 62065943. OCLC 7419446
- ↑ a b Klein, Herbert Arthur (2012) [1988, 1974]. «Chapter 8: Keeping Track of Time». The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology). Col: Dover Books on Mathematics reimpressção corrigida do original ed. [S.l.]: Dover Publications, Inc. / Courier Corporation (originalmente por Simon & Schuster, Inc.). p. 102. ISBN 978-0-48614497-9. LCCN 88-25858. Consultado em 6 de agosto de 2019
- ↑ Croxton, Frederick E. (1922). «A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams"». Journal of the American Statistical Association. Short Note. 18 (137): 108–109. doi:10.1080/01621459.1922.10502455
- ↑ Schiffner, Friedrich (1965). Wähnl, Maria Emma, ed. «Bestimmung von Satellitenbahnen». Wien, Austria: Volksbildungshaus Wiener Urania. Astronomische Mitteilungen der Urania-Sternwarte Wien (em alemão). 8
- ↑ Hayes, Eugene Nelson (1975) [1968]. Trackers of the Skies. Col: History of the Smithsonian Satellite-tracking Program. Cambridge, Massachusetts, USA: Academic Press / Howard A. Doyle Publishing Company
- ↑ «ooPIC Programmer's Guide - Chapter 15: URCP». ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007 [1997]. Consultado em 5 de agosto de 2019. Arquivado do original em 28 de junho de 2008
- ↑ Hargreaves, Shawn. «Angles, integers, and modulo arithmetic». blogs.msdn.com. Consultado em 5 de agosto de 2019. Cópia arquivada em 30 de junho de 2019
- ↑ Sloane, N. J. A. (ed.). «Sequência A019692 (Decimal expansion of 2*Pi)». On-Line Encyclopedia of Integer Sequences (em inglês). OEIS Foundation
Ligações externas
editar- «Manifesto tau» (em inglês)